C
分析:根据旋转的性质得∠ABA
1=∠CBC
1=α,∠C
1=∠C,BC=BC
1,而∠DFC=∠BFC
1,根据三角形内角和定理可得∠CDF+∠C=∠FBC
1+∠C
1,则∠CDF=α;利用AB=BC旋转的性质得BA=BC
1,∠A=∠C=∠C
1,然后根据“ASA”可判断△BAE≌△BC
1F,所以BE=BF;利用BA=BA
1=BC,得BA
1-BE=BC-BF,即A
1E=CF;由于∠CDF=α,是变化的角,则∠CDF≠∠C,
于是DF≠FC.
解答:∵将△ABC绕点B顺时针旋转α度,得到△A
1BC
1,
∴∠ABA
1=∠CBC
1=α,∠C
1=∠C,BC=BC
1,
∵∠DFC=∠BFC
1,
∴∠CDF+∠C=∠FBC
1+∠C
1,
∴∠CDF=α,所以①正确;
∵AB=BC,
∴BA=BC
1,∠A=∠C=∠C
1,
在△BAE和△BC
1F中,
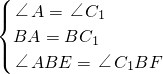
,
∴△BAE≌△BC
1F,
∴BE=BF,所以④正确;
∵BA=BA
1=BC,
∴BA
1-BE=BC-BF,
∴A
1E=CF;所以②正确;
∵∠CDF=α,
∴∠CDF≠∠C,
∴DF≠FC,所以③错误.
故选C.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.

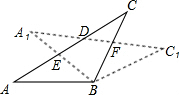 如图,在△ABC中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC,BC于点D,F,下列结论:
如图,在△ABC中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC,BC于点D,F,下列结论: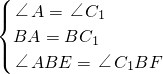 ,
,

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为