
����Ŀ����ͼ����֪��ABC �У�AB=AC=6cm����B=��C��BC=4cm���� D Ϊ AB���е㣮
��1������� P ���߶� BC ���� 1cm/s ���ٶ��ɵ� B ��� C �˶���ͬʱ���� Q ���߶� CA ���ɵ� C ��� A �˶���
������ Q ���˶��ٶ���� P ���˶��ٶ���ȣ����� 1 �����BPD ����CQP �Ƿ�ȫ�ȣ���˵�����ɣ�
������ Q ���˶��ٶ���� P ���˶��ٶȲ���ȣ����� Q ���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD ����CQP ȫ�ȣ�
��2������ Q �Ԣ��е��˶��ٶȴӵ� C �������� P ��ԭ�����˶��ٶȴӵ� B ͬʱ����������ʱ���ء�ABC �����˶����� �� P ��� Q ��һ���ڡ�ABC �� �������������ں�����ֱ��д���𰸣�������д������̣�

���𰸡���1����ȫ�ȣ����ɼ�������1��5cm/s���ɼ�������2��24s����AC������
��������
���⣨1��������ʱ����ٶȷֱ����������������BP��CQ��BD��PC�ߵij�������SAS�ж�����������ȫ�ȣ�
������ȫ��������Ӧ���������̽���֮��Ĺ�ϵ���ٸ���·��=�ٶ���ʱ�乫ʽ������õ�P�˶���ʱ�䣬����õ�Q���˶��ٶȣ�
��2������������ͼ�η������֣����ڵ�Q���ٶȿ죬���ڵ�P��ǰ�ߣ�����Ҫ���һ����������Ӧ�ñȵ�P���ߵ��������ε������߳���
�⣺��1����ȫ�ȣ��������£�
��t=1�룬
��BP=CQ=1��1=1���ף�
��AB=6cm����DΪAB���е㣬
��BD=3cm��
����PC=BC��BP��BC=4cm��
��PC=4��1=3cm��
��PC=BD��
����AB=AC��
���B=��C��
���BPD�ա�CQP��
��������BPD�ա�CQP��
��vP��vQ��
��BP��CQ��
���ߡ�BPD�ա�CQP����B=��C����BP=CP=2��BD=CQ=3��
����P����Q�˶���ʱ��t=![]() =2�룬
=2�룬
��vQ=![]() ==1.5cm/s��
==1.5cm/s��
��2���辭��x����P���Q��һ��������
�����⣬�� 1.5x=x+2��6��
���x=24��
����P���˶���24s��1cm/s=24cm��
��24=2��12��
����P����Q��AC����������
������24���P���Q��һ���ڱ�AC��������




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ���ڵ����ϵĵ��߸�AB��������������ˮƽ����������ϵ�Ӱ�ӷֱ���BC��CD�����BC=6�ף�CD=4�ף���BCD=150�㣬��D����õ��߸˶���A������Ϊ30�㣬������߸˵ĸ߶ȣ�����������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������ε��ܳ�Ϊ28cm�����е�һ�߳�����һ�߳���![]() ������������������θ��ߵij���
������������������θ��ߵij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB��ֱ�������Σ���AOB=90�㣬OB=2OA����A�ڷ���������y= ![]() ��ͼ���ϣ�����B�ڷ���������y=
��ͼ���ϣ�����B�ڷ���������y= ![]() ��ͼ���ϣ���k��ֵΪ ��
��ͼ���ϣ���k��ֵΪ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
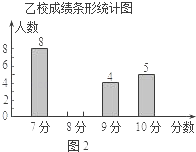
����Ŀ���ס�����У�μ��������־ٰ��ѧ��Ӣ����ᄎ������У����������ȣ�������������ѧ���ɼ��ֱ�Ϊ7�֡�8�֡�9�֡�10�֣�����Ϊ10�֣�������ͳ�����ݻ����������в�������ͳ��ͼ���� 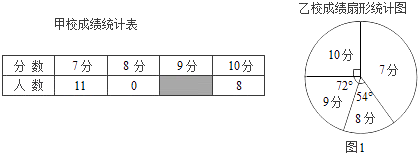
��1����ͼ1�У���7�֡��������ε�Բ�Ľǵ����㣮
��2�����㽫ͼ2��ͳ��ͼ����������
��3�������㣬��У��ƽ������8.3�֣���λ����8�֣���д����У��ƽ���֡���λ��������ƽ���ֺ���λ���ĽǶȷ����ĸ�ѧУ�ɼ��Ϻã�
��4������ý�����Ҫ��֯8�˵Ĵ����Ӳμ��м���������Ϊ���ڹ�����������������ѧУ�е�һ����ѡ����ѡ�֣����������Ӧѡ����ѧУ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ACD����ABC����ǣ���A=40�㣬BEƽ�֡�ABC��CEƽ�֡�ACD����BE��CE���ڵ�E��
��1�����E�Ķ�����
��2��������A���E֮���������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������У�����֤����ABC�ա�DCB�� ��������

A. AB=DC��AC=DB B. AB=DC����ABC=��DCB
C. DB=AC����DBC=��ACB D. DC=AB����DBC=��ACB
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�У�AB=AC��
��1����ͼ1���ڡ�ADE�У���AD=AE���ҡ�DAE=��BAC����֤��CD=BE��
��2����ͼ2���ڡ�ADE�У�����DAE=��BAC=60�㣬��CD��ֱƽ��AE��AD=3��CD=4����BD�ij���
��3����ͼ3���ڡ�ADE�У���BD��ֱƽ��AE��H���ҡ�BAC=2��ADBʱ����̽��CD2��BD2��AH2֮���������ϵ����֤����
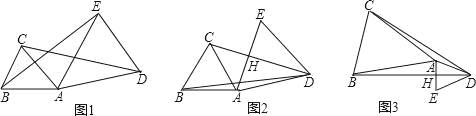
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУѧ�����������,�����ȡ��У����������Ů�����г�������.��֪��ȡ��������,������Ů��������ͬ,�����������ݻ�������ͳ�Ʊ���ͳ��ͼ(��ͼ20-3-2��ʾ):
������������(��λ:cm)
��� | ���� |
A | x��155 |
B | 155��x��160 |
C | 160��x��165 |
D | 165��x��170 |
E | x��170 |
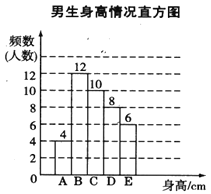
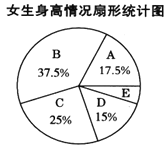
����ͼ���ṩ����Ϣ,�ش���������:
(1)������,�������ߵ�������___________��,��λ����___________�飻
(2)������,Ů��������E�����___________�ˣ�
(3)��֪��У��������400�ˡ�Ů��380��,�����������160��x��170��Χ�ڵ�ѧ��Լ�ж�����.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com