
如图,直线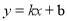 与x轴交于点A(1,0),与 y交于点B(0,-2).
与x轴交于点A(1,0),与 y交于点B(0,-2).
(1)求直线AB的表达式;
(2)点C是直线AB上的点,且CA=AB,过动点P(m,0)且垂直于x轴的直线与直线AB 交于点D,若点D不在线段BC上,写出m的取值范围.
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源:【全国校级联考】广东省深州市2017届初三七校联考数学试卷 题型:解答题
四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的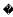 O过点E.
O过点E.
(1)求证:四边形ABCD是菱形.
(2)若CD的延长线与圆相切于点F,已知直径AB=4.求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源:【全国校级联考】广东省深州市2017届初三七校联考数学试卷 题型:单选题
一个盒子装有除颜色外其它均相同的2个红球和1个白球,现从中任取2个球,则取到的是一个红球、一个白球的概率为().
A. 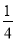 B.
B. 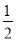 C.
C. 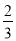 D.
D. 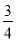
查看答案和解析>>
科目:初中数学 来源:【全国区级联考】北京市燕山区2017届九年级一模考试数学试卷 题型:解答题
有这样一个问题:探究函数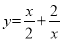 的图象和性质.小奥根据学习函数的经验,对函数
的图象和性质.小奥根据学习函数的经验,对函数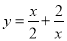 的图象和性质进行了探究.下面是小奥的探究过程,请补充完整:
的图象和性质进行了探究.下面是小奥的探究过程,请补充完整:
(1)函数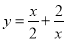 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值:

求m的值;
(3)如下图,在平面直角坐标系xoy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,2).结合函数图象,写出该函数的其他性质(一条即可): .

查看答案和解析>>
科目:初中数学 来源:【全国区级联考】北京市燕山区2017届九年级一模考试数学试卷 题型:填空题
下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.
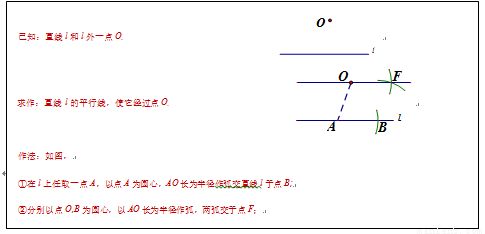
请回答:该作图依据是__________________________________________________.
查看答案和解析>>
科目:初中数学 来源:【全国区级联考】北京市燕山区2017届九年级一模考试数学试卷 题型:单选题
2017 全英羽毛球公开赛混双决赛,中国组合鲁恺 / 黄雅琼,对阵马来西亚里约奥运亚军陈炳顺/吴柳萤,鲁恺/黄雅琼两名小将的完美配合结果获胜.如图是羽毛球场地示意图,x 轴平行场地的中线,y 轴平行场地的球网线,设定鲁恺的坐标是(3,1),黄雅琼的坐标是(0,-1),则坐标原点为( )
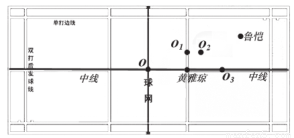
A. O B. 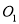 C.
C. 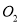 D.
D. 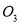
查看答案和解析>>
科目:初中数学 来源:福建省2016-2017学年七年级(下)期末模拟数学试卷 题型:填空题
为了解我校八年级同学的视力情况,从中随机抽查了30名学生的视力.在这个问题中,样本是__.
查看答案和解析>>
科目:初中数学 来源:【全国区级联考】江西省广丰区2017届初三中考模拟(一)数学试卷 题型:解答题
【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com