
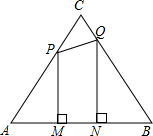
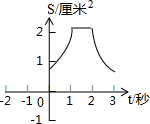
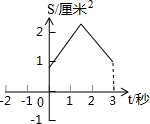
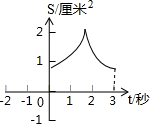
 如图,等边△ABC的边长为4厘米,长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B时运动终止),过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点.设线段MN运动的时间为t秒,四边形MNQP的面积为S厘米2.则表示S与t的函数关系的图象大致是
如图,等边△ABC的边长为4厘米,长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B时运动终止),过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点.设线段MN运动的时间为t秒,四边形MNQP的面积为S厘米2.则表示S与t的函数关系的图象大致是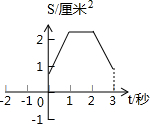
 AB,然后分:①点N在AD上时,P、Q都在AC上,利用∠A的正切值表示出PM、QN,然后根据梯形的面积公式列式整理即可得到S与t的函数关系式;②点N在BD上,点M在AD上时,点P在在AC上,点Q在BC上,先表示出AM、BN,再利用∠A、∠B的正切值表示出PM、QN,然后根据梯形的面积公式列式整理即可得到S与t的函数关系式;③点M在BD上时,点P、Q都在BC上,利用∠B的正切值表示出PM、QN,然后根据梯形的面积公式列式整理即可得到S与t的函数关系式.
AB,然后分:①点N在AD上时,P、Q都在AC上,利用∠A的正切值表示出PM、QN,然后根据梯形的面积公式列式整理即可得到S与t的函数关系式;②点N在BD上,点M在AD上时,点P在在AC上,点Q在BC上,先表示出AM、BN,再利用∠A、∠B的正切值表示出PM、QN,然后根据梯形的面积公式列式整理即可得到S与t的函数关系式;③点M在BD上时,点P、Q都在BC上,利用∠B的正切值表示出PM、QN,然后根据梯形的面积公式列式整理即可得到S与t的函数关系式.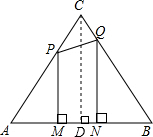 解:如图,过点C作CD⊥AB于D,
解:如图,过点C作CD⊥AB于D, AB=
AB= ×4=2,
×4=2, t,QN=AN•tan60°=
t,QN=AN•tan60°= (t+1)=
(t+1)= t+
t+ ,
, (
( t+
t+ t+
t+ )=
)= t+
t+ ;
; t,QN=BN•tan60°=
t,QN=BN•tan60°= (3-t)=3
(3-t)=3 -
- t,
t, (
( t+3
t+3 -
- t)=
t)= ;
; (4-t)=4
(4-t)=4 -
- t,QN=BN•tan60°=
t,QN=BN•tan60°= (3-t)=3
(3-t)=3 -
- t,
t, (4
(4 -
- t+3
t+3 -
- t)=-
t)=- t+
t+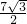 ;
;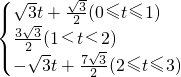 ,
,

科目:初中数学 来源: 题型:
 如图,等边△ABC的边长为l,取边AC的中点D,在外部画出一个新的等边三角形△CDE,如此绕点C顺时针继续下去,直到所画等边三角形的一边与△ABC的BC边重叠为止,此时这个三角形的边长为
如图,等边△ABC的边长为l,取边AC的中点D,在外部画出一个新的等边三角形△CDE,如此绕点C顺时针继续下去,直到所画等边三角形的一边与△ABC的BC边重叠为止,此时这个三角形的边长为查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,等边△ABC的边长为6,点D、E分别在AB、AC上,且AD=AE=2,直线l过点A,且l∥BC,若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设F点运动的时间为t秒,当t>0时,直线DF交l于点G,GE的延长线与BC的延长线交于点H,AB与GH相交于点O.
已知:如图,等边△ABC的边长为6,点D、E分别在AB、AC上,且AD=AE=2,直线l过点A,且l∥BC,若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设F点运动的时间为t秒,当t>0时,直线DF交l于点G,GE的延长线与BC的延长线交于点H,AB与GH相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:
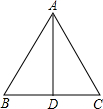 如图,等边△ABC的边长为2,AD是△ABC的角平分线,
如图,等边△ABC的边长为2,AD是△ABC的角平分线,查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为( )
如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com