已知抛物线m:y=ax2+2ax+a-1,顶点为A,若将抛物线m绕着点(1,0)旋转180°后得到抛物线n,顶点为C.
(1)当a=1时.试求抛物线n的顶点C的坐标,再求它的解析式;
(2)在(1)中,请你分别在抛物线m、n上各取一点D、B(除点A、C外),使得四边形ABCD为平行四边形(直接写出所取点的坐标,并至少写出二种情况);
(3)设抛物线m的对称轴与抛物线n的交点为P,且|AP|=6,试求a的值.
解:(1)当a=1时,抛物线m的解析式为y=x
2+2x,A(-1,-1),
当点A(-1,-1)绕着点(1,0)旋转180°后所得点C坐标为(3,1),
根据题意,可得抛物线n的解析式为y=-(x-3)
2+1,
即y=-x
2+6x-8;
(2)如:D(-2,0)与B(4,0)或D(0,0)与B(2,0)或D(-3,3)与B(5,-3).(答案不唯一)
(3)抛物线n的解析式可表示为y=-a(x-3)
2+1,
即y=-ax
2+6ax-9a+1,
∵A(-1,-1),当x=-1时,y=-a-6a-9a+1=-16a+1,
∴|-1-(-16a+1)|=6,
当16a-2=6时,16a=8,a=

,
当16a-2=-6时,16a=-4,a=

,
∴

或
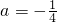
.
分析:(1)先根据旋转的性质得出抛物线n的方程,将a的值代入抛物线方程中,利用顶点公式即可得出C的坐标;
(2)欲使四边形ABCD为平行四边形,利用平行四边形的性质即可直接得出D和B点的坐标;
(3)先将抛物线的方程化为顶点式,将A的坐标代入,可得出a的值(注意A的值有两个).
点评:本题主要考查了二次函数解析式的确定、函数图象旋转的性质等知识点,关键是要得出旋转后的函数解析式.

 ,
, ,
, 或
或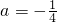 .
.

 名校课堂系列答案
名校课堂系列答案 正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为
正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为 廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-
廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-