
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§÷±œΏy= ![]() x+2”κx÷αΫΜ”ΎΒψAΘ§”κy÷αΫΜ”ΎΒψCΘ§≈ΉΈοœΏy=
x+2”κx÷αΫΜ”ΎΒψAΘ§”κy÷αΫΜ”ΎΒψCΘ§≈ΉΈοœΏy= ![]() x2+bx+cΨ≠ΙΐAΓΔCΝΫΒψΘ§”κx÷αΒΡΝμ“ΜΫΜΒψΈΣΒψBΘ°
x2+bx+cΨ≠ΙΐAΓΔCΝΫΒψΘ§”κx÷αΒΡΝμ“ΜΫΜΒψΈΣΒψBΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®2Θ©ΒψDΈΣ÷±œΏAC…œΖΫ≈ΉΈοœΏ…œ“ΜΕ·ΒψΘΜ
ΔΌΝ§Ϋ”BCΓΔCDΘ§…η÷±œΏBDΫΜœΏΕΈAC”ΎΒψEΘ§ΓςCDEΒΡΟφΜΐΈΣS1 Θ§ ΓςBCEΒΡΟφΜΐΈΣS2 Θ§ «σ ![]() ΒΡΉν¥σ÷ΒΘΜ
ΒΡΉν¥σ÷ΒΘΜ
ΔΎΙΐΒψDΉςDFΓΆACΘ§¥ΙΉψΈΣΒψFΘ§Ν§Ϋ”CDΘ§ «Ζώ¥φ‘ΎΒψDΘ§ ΙΒΟΓςCDF÷–ΒΡΡ≥ΗωΫ««ΓΚΟΒ»”ΎΓœBACΒΡ2±ΕΘΩ»τ¥φ‘ΎΘ§«σΒψDΒΡΚαΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©
ΫβΘΚΗυΨίΧβ“βΒΟAΘ®©¹4Θ§0Θ©Θ§CΘ®0Θ§2Θ©Θ§
ΓΏ≈ΉΈοœΏy=©¹ ![]() x2+bx+cΨ≠ΙΐAΓΔCΝΫΒψΘ§
x2+bx+cΨ≠ΙΐAΓΔCΝΫΒψΘ§
Γύ 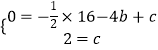 Θ§
Θ§
Γύ 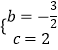 Θ§
Θ§
Γύy=©¹ ![]() x2©¹
x2©¹ ![]() x+2
x+2
Θ®2Θ©
ΫβΘΚΔΌ»γΆΦΘ§
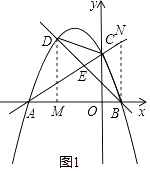
Ννy=0Θ§
Γύ©¹ ![]() x2©¹
x2©¹ ![]() x+2=0Θ§
x+2=0Θ§
Γύx1=©¹4Θ§x2=1Θ§
ΓύBΘ®1Θ§0Θ©Θ§
ΙΐDΉςDMΓΆx÷α”ΎMΘ§ΙΐBΉςBNΓΆx÷αΫΜ”ΎAC”ΎNΘ§
ΓύDMΓΈBNΘ§
ΓύΓςDMEΓΉΓςBNEΘ§
Γύ ![]() =
= ![]() =
= ![]() Θ§
Θ§
…ηDΘ®aΘ§=©¹ ![]() a2©¹
a2©¹ ![]() a+2Θ©Θ§
a+2Θ©Θ§
ΓύMΘ®aΘ§ ![]() a+2Θ©Θ§
a+2Θ©Θ§
ΓΏBΘ®1.0Θ©Θ§
ΓύNΘ®1Θ§ ![]() Θ©Θ§
Θ©Θ§
Γύ ![]() =
= ![]() =
= 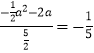 Θ®a+2Θ©2+
Θ®a+2Θ©2+ ![]() ΘΜ
ΘΜ
ΓύΒ±a=2 ±Θ§ ![]() ΒΡΉν¥σ÷Β «
ΒΡΉν¥σ÷Β « ![]() ΘΜ
ΘΜ
ΔΎΓΏAΘ®©¹4Θ§0Θ©Θ§BΘ®1Θ§0Θ©Θ§CΘ®0Θ§2Θ©Θ§
ΓύAC=2 ![]() Θ§BC=
Θ§BC= ![]() Θ§AB=5Θ§
Θ§AB=5Θ§
ΓύAC2+BC2=AB2Θ§
ΓύΓςABC «“‘ΓœACBΈΣ÷±Ϋ«ΒΡ÷±Ϋ«»ΐΫ«–ΈΘ§»ΓABΒΡ÷–ΒψPΘ§
ΓύPΘ®©¹ ![]() Θ§0Θ©Θ§
Θ§0Θ©Θ§
ΓύPA=PC=PB= ![]() Θ§
Θ§
ΓύΓœCPO=2ΓœBACΘ§
ΓύtanΓœCPO=tanΘ®2ΓœBACΘ©= ![]() Θ§
Θ§
ΙΐΉςx÷αΒΡΤΫ––œΏΫΜy÷α”ΎRΘ§ΫΜACΒΡ―”≥ΛœΏ”ΎGΘ§
«ιΩω“ΜΘΚ»γΆΦΘ§
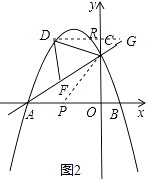
ΓύΓœDCF=2ΓœBAC=ΓœDGC+ΓœCDGΘ§
ΓύΓœCDG=ΓœBACΘ§
ΓύtanΓœCDG=tanΓœBAC= ![]() Θ§
Θ§
Φ¥ ![]() Θ§
Θ§
ΝνDΘ®aΘ§©¹ ![]() a2©¹
a2©¹ ![]() a+2Θ©Θ§
a+2Θ©Θ§
ΓύDR=©¹aΘ§RC=©¹ ![]() a2©¹
a2©¹ ![]() aΘ§
aȧ
Γύ ![]() Θ§
Θ§
Γύa1=0Θ®…α»ΞΘ©Θ§a2=©¹2Θ§
ΓύxD=©¹2Θ§
«ιΩωΕΰΘ§ΓύΓœFDC=2ΓœBACΘ§
ΓύtanΓœFDC= ![]() Θ§
Θ§
…ηFC=4kΘ§
ΓύDF=3kΘ§DC=5kΘ§
ΓΏtanΓœDGC= ![]() =
= ![]() Θ§
Θ§
ΓύFG=6kΘ§
ΓύCG=2kΘ§DG=3 ![]() kΘ§Γύ
kΘ§Γύ
ΓύRC= ![]() kΘ§RG=
kȧRG= ![]() kȧ
kȧ
DR=3 ![]() k©¹
k©¹ ![]() k=
k= ![]() kȧ
kȧ
Γύ ![]() =
= ![]() =
= ![]() Θ§
Θ§
Γύa1=0Θ®…α»ΞΘ©Θ§a2= ![]() Θ§
Θ§
ΒψDΒΡΚαΉχ±ξΈΣ©¹2Μρ©¹ ![]() Θ°
Θ°
ΓΨΫβΈωΓΩΘ®1Θ©ΗυΨίΧβ“βΒΟΒΫAΘ®©¹4Θ§0Θ©Θ§CΘ®0Θ§2Θ©¥ζ»κy=©¹ ![]() x2+bx+cΘ§”Ύ «ΒΟΒΫΫα¬έΘΜΘ®2Θ©ΔΌ»γΆΦΘ§Ννy=0Θ§ΫβΖΫ≥ΧΒΟΒΫx1=©¹4Θ§x2=1Θ§«σΒΟBΘ®1Θ§0Θ©Θ§ΙΐDΉςDMΓΆx÷α”ΎMΘ§ΙΐBΉςBNΓΆx÷αΫΜ”ΎAC”ΎNΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…ΒΟΒΫΫα¬έΘΜΔΎΗυΨίΙ¥Ι…Ε®άμΒΡΡφΕ®άμΒΟΒΫΓςABC «“‘ΓœACBΈΣ÷±Ϋ«ΒΡ÷±Ϋ«»ΐΫ«–ΈΘ§»ΓABΒΡ÷–ΒψPΘ§«σΒΟPΘ®©¹
x2+bx+cΘ§”Ύ «ΒΟΒΫΫα¬έΘΜΘ®2Θ©ΔΌ»γΆΦΘ§Ννy=0Θ§ΫβΖΫ≥ΧΒΟΒΫx1=©¹4Θ§x2=1Θ§«σΒΟBΘ®1Θ§0Θ©Θ§ΙΐDΉςDMΓΆx÷α”ΎMΘ§ΙΐBΉςBNΓΆx÷αΫΜ”ΎAC”ΎNΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…ΒΟΒΫΫα¬έΘΜΔΎΗυΨίΙ¥Ι…Ε®άμΒΡΡφΕ®άμΒΟΒΫΓςABC «“‘ΓœACBΈΣ÷±Ϋ«ΒΡ÷±Ϋ«»ΐΫ«–ΈΘ§»ΓABΒΡ÷–ΒψPΘ§«σΒΟPΘ®©¹ ![]() Θ§0Θ©Θ§ΒΟΒΫPA=PC=PB=
Θ§0Θ©Θ§ΒΟΒΫPA=PC=PB= ![]() Θ§ΙΐΉςx÷αΒΡΤΫ––œΏΫΜy÷α”ΎRΘ§ΫΜACΒΡ―”œΏ”ΎGΘ§«ιΩω“ΜΘΚ»γΆΦΘ§ΓœDCF=2ΓœBAC=ΓœDGC+ΓœCDGΘ§«ιΩωΕΰΘ§ΓœFDC=2ΓœBACΘ§Ϋβ÷±Ϋ«»ΐΫ«–ΈΦ¥Ω…ΒΟΒΫΫα¬έΘ°
Θ§ΙΐΉςx÷αΒΡΤΫ––œΏΫΜy÷α”ΎRΘ§ΫΜACΒΡ―”œΏ”ΎGΘ§«ιΩω“ΜΘΚ»γΆΦΘ§ΓœDCF=2ΓœBAC=ΓœDGC+ΓœCDGΘ§«ιΩωΕΰΘ§ΓœFDC=2ΓœBACΘ§Ϋβ÷±Ϋ«»ΐΫ«–ΈΦ¥Ω…ΒΟΒΫΫα¬έΘ°
ΓΨΩΦΒψΨΪΈωΓΩ±ΨΧβ÷ς“ΣΩΦ≤ιΝΥΕΰ¥ΈΚ· ΐΒΡ–‘÷ ΒΡœύΙΊ÷Σ ΕΒψΘ§–η“Σ’ΤΈ’‘ωΦθ–‘ΘΚΒ±a>0 ±Θ§Ε‘≥Τ÷αΉσ±ΏΘ§yΥφx‘ω¥σΕχΦθ–ΓΘΜΕ‘≥Τ÷α”“±ΏΘ§yΥφx‘ω¥σΕχ‘ω¥σΘΜΒ±a<0 ±Θ§Ε‘≥Τ÷αΉσ±ΏΘ§yΥφx‘ω¥σΕχ‘ω¥σΘΜΕ‘≥Τ÷α”“±ΏΘ§yΥφx‘ω¥σΕχΦθ–Γ≤≈Ρή’ΐ»ΖΫβ¥π¥ΥΧβΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫ»Υ‘Ύ1800ΟΉ≥ΛΒΡ÷±œΏΒά¬Ζ…œ≈ή≤ΫΘ§ΦΉΓΔ““ΝΫ»ΥΆ§ΤπΒψΓΔΆ§ΖΫœρ≥ωΖΔΘ§≤ΔΖ÷±π“‘≤ΜΆ§ΒΡΥΌΕ»‘»ΥΌ«ΑΫχΘ°“―÷ΣΘ§ΦΉ≥ωΖΔ30ΟκΚσΘ§““≥ωΖΔΘ§““ΒΫ÷’ΒψΚσΝΔΦ¥ΖΒΜΊΘ§≤Δ“‘‘≠ά¥ΒΡΥΌΕ»«ΑΫχΘ§ΉνΚσ”κΦΉœύ”ωΘ§¥Υ ±≈ή≤ΫΫα χΘ°»γΆΦΘ§yΘ®ΟΉΘ©±μ ΨΦΉΓΔ““ΝΫ»Υ÷°ΦδΒΡΨύάκΘ§tΘ®ΟκΘ©±μ ΨΦΉ≥ωΖΔΒΡ ±ΦδΘ§ΆΦ÷–’έœΏΦΑ ΐΨί±μ Ψ’ϊΗω≈ή≤ΫΙΐ≥Χ÷–y”κtΚ· ΐΙΊœΒΘ°Ρ«Ο¥Θ§““ΒΫ÷’ΒψΚσΟκ”κΦΉœύ”ωΘ° 
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΓΑΚξ―ο¥ΪΆ≥ΈΡΜ·Θ§¥ρ‘λ ιœψ–Θ‘ΑΓ±ΜνΕ·÷–Θ§―ß–ΘΦΤΜ°ΩΣ’ΙΥΡœνΜνΕ·ΘΚΓΑA©¹Ιζ―ßΥ–ΕΝΓ±ΓΔΓΑB©¹―ίΫ≤Γ±ΓΔΓΑC©¹ΩΈ±ΨΨγΓ±ΓΔΓΑD©¹ ιΖ®Γ±Θ§“Σ«σΟΩΈΜΆ§―ß±Ί–κ«“÷ΜΡή≤ΈΦ”Τδ÷–“ΜœνΜνΕ·Θ§―ß–ΘΈΣΝΥΝΥΫβ―ß…ζΒΡ“β‘ΗΘ§ΥφΜζΒς≤ιΝΥ≤ΩΖ÷―ß…ζΘ§ΫαΙϊΆ≥ΦΤ»γœ¬ΘΚ 
Θ®1Θ©»γΆΦΘ§œΘΆϊ≤ΈΦ”ΜνΕ·C’Φ20%Θ§œΘΆϊ≤ΈΦ”ΜνΕ·B’Φ15%Θ§‘ρ±ΜΒς≤ιΒΡΉή»Υ ΐΈΣ»ΥΘ§…»–ΈΆ≥ΦΤΆΦ÷–Θ§œΘΆϊ≤ΈΦ”ΜνΕ·DΥυ’Φ‘≤–ΡΫ«ΈΣΕ»Θ§ΗυΨίΧβ÷––≈œΔ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘ°
Θ®2Θ©―ß–Θœ÷”–800Οϊ―ß…ζΘ§«κΗυΨίΆΦ÷––≈œΔΘ§ΙάΥψ»Ϊ–Θ―ß…ζœΘΆϊ≤ΈΦ”ΜνΕ·A”–Εύ…Ό»ΥΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ –ΈΣ¥¥Ϋ®»ΪΙζΈΡΟς≥« –Θ§ΩΣ’ΙΓΑΟάΜ·¬ΧΜ·≥« –Γ±ΜνΕ·Θ§ΦΤΜ°Ψ≠Ιΐ»τΗ…Ρξ Ι≥««χ¬ΧΜ·ΉήΟφΜΐ–¬‘ω360ΆρΤΫΖΫΟΉΘ°Ή‘2013Ρξ≥θΩΣ Φ Β ©ΚσΘ§ ΒΦ ΟΩΡξ¬ΧΜ·ΟφΜΐ «‘≠ΦΤΜ°ΒΡ1.6±ΕΘ§’β―υΩ…Χα«Α4ΡξΆξ≥…»ΈΈώΘ°
Θ®1Θ©Έ ΒΦ ΟΩΡξ¬ΧΜ·ΟφΜΐΕύ…ΌΆρΤΫΖΫΟΉΘΩ
Θ®2Θ©ΈΣΦ”¥σ¥¥≥«ΝΠΕ»Θ§ –’ΰΗ°ΨωΕ®¥”2016ΡξΤπΦ”Ωλ¬ΧΜ·ΥΌΕ»Θ§“Σ«σ≤Μ≥§Ιΐ2ΡξΆξ≥…Θ§Ρ«Ο¥ ΒΦ ΤΫΨυΟΩΡξ¬ΧΜ·ΟφΜΐ÷Ν…ΌΜΙ“Σ‘ωΦ”Εύ…ΌΆρΤΫΖΫΟΉΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΨΊ–ΈABCD÷–Θ§ΓœABDΓΔΓœCDBΒΡΤΫΖ÷œΏBEΓΔDFΖ÷±πΫΜ±ΏADΓΔBC”ΎΒψEΓΔFΘ° 
Θ®1Θ©«σ÷ΛΘΚΥΡ±Ώ–ΈBEDF «ΤΫ––ΥΡ±Ώ–ΈΘΜ
Θ®2Θ©Β±ΓœABEΈΣΕύ…ΌΕ» ±Θ§ΥΡ±Ώ–ΈBEDF «Νβ–ΈΘΩ«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥Χε”ΐάœ Π≤βΝΩΝΥΉ‘ΦΚ»ΈΫΧΒΡΦΉΓΔ““ΝΫΑύΡ–…ζΒΡ…μΗΏΘ§≤Δ÷ΤΉςΝΥ»γœ¬≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦ±μΘ°
…μΗΏΖ÷Ήι | ΤΒ ΐ | ΤΒ¬ |
152ΓήxΘΦ155 | 3 | 0.06 |
155ΓήxΘΦ158 | 7 | 0.14 |
158ΓήxΘΦ161 | m | 0.28 |
161ΓήxΘΦ164 | 13 | n |
164ΓήxΘΦ167 | 9 | 0.18 |
167ΓήxΘΦ170 | 3 | 0.06 |
170ΓήxΘΦ173 | 1 | 0.02 |

ΗυΨί“‘…œΆ≥ΦΤΆΦ±μΆξ≥…œ¬Ν–Έ ΧβΘΚ
Θ®1Θ©Ά≥ΦΤ±μ÷–m= Θ§ n= Θ§ ≤ΔΫΪΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®2Θ©‘Ύ’β¥Έ≤βΝΩ÷–ΝΫΑύΡ–…ζ…μΗΏΒΡ÷–ΈΜ ΐ‘ΎΘΚΖΕΈßΡΎΘΜ
Θ®3Θ©‘Ύ…μΗΏΓί167cmΒΡ4»Υ÷–Θ§ΦΉΓΔ““ΝΫΑύΗς”–2»ΥΘ§œ÷¥”4»Υ÷–ΥφΜζΆΤ―Γ2»Υ≤Ι≥δΒΫ―ß–ΘΙζΤλΜΛΈάΕ”÷–Θ§«κ”ΟΝ–±μΜρΜ≠ ςΉ¥ΆΦΒΡΖΫΖ®«σ≥ω’βΝΫ»ΥΕΦά¥Ή‘œύΆ§ΑύΦΕΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕΰ¥ΈΚ· ΐy=ax2+bx+cΘ®ΓΌ0Θ©ΒΡΆΦœσ»γΆΦΘ§Ηχ≥ωœ¬Ν–ΥΡΗωΫα¬έΘΚΔΌ4ac©¹b2ΘΦ0ΘΜΔΎ3b+2cΘΦ0ΘΜΔέ4a+cΘΦ2bΘΜΔήmΘ®am+bΘ©+bΘΦaΘ®mΓΌ1Θ©Θ§Τδ÷–Ϋα¬έ’ΐ»ΖΒΡΗω ΐ «Θ® Θ© 
A.1
B.2
C.3
D.4
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§OΈΣ‘≠ΒψΘ§ΥΡ±Ώ–ΈABCO «ΨΊ–ΈΘ§ΒψAΘ§CΒΡΉχ±ξΖ÷±π «AΘ®0Θ§2Θ©ΚΆCΘ®2 ![]() Θ§0Θ©Θ§ΒψD «Ε‘Ϋ«œΏAC…œ“ΜΕ·ΒψΘ®≤Μ”κAΘ§C÷ΊΚœΘ©Θ§Ν§ΫαBDΘ§ΉςDEΓΆDBΘ§ΫΜx÷α”ΎΒψEΘ§“‘œΏΕΈDEΘ§DBΈΣΝΎ±ΏΉςΨΊ–ΈBDEFΘ°
Θ§0Θ©Θ§ΒψD «Ε‘Ϋ«œΏAC…œ“ΜΕ·ΒψΘ®≤Μ”κAΘ§C÷ΊΚœΘ©Θ§Ν§ΫαBDΘ§ΉςDEΓΆDBΘ§ΫΜx÷α”ΎΒψEΘ§“‘œΏΕΈDEΘ§DBΈΣΝΎ±ΏΉςΨΊ–ΈBDEFΘ°
Θ®1Θ©ΧνΩ’ΘΚΒψBΒΡΉχ±ξΈΣΘΜ
Θ®2Θ© «Ζώ¥φ‘Ύ’β―υΒΡΒψDΘ§ ΙΒΟΓςDEC «Β»―ϋ»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωADΒΡ≥ΛΕ»ΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
Θ®3Θ©ΔΌ«σ÷ΛΘΚ ![]() =
= ![]() ΘΜ
ΘΜ
ΔΎ…ηAD=xΘ§ΨΊ–ΈBDEFΒΡΟφΜΐΈΣyΘ§«σyΙΊ”ΎxΒΡΚ· ΐΙΊœΒ ΫΘ®Ω…άϊ”ΟΔΌΒΡΫα¬έΘ©Θ§≤Δ«σ≥ωyΒΡΉν–Γ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΨΊ–ΈOABCΒΡΕΞΒψO”κΉχ±ξ‘≠Βψ÷ΊΚœΘ§ΕΞΒψAΘ§CΖ÷±π‘ΎΉχ±ξ÷α…œΘ§ΕΞΒψBΒΡΉχ±ξΈΣΘ®4Θ§2Θ©Θ°ΙΐΒψDΘ®0Θ§3Θ©ΚΆEΘ®6Θ§0Θ©ΒΡ÷±œΏΖ÷±π”κABΘ§BCΫΜ”ΎΒψMΘ§NΘ°
Θ®1Θ©«σΙΐOΘ§BΘ§E»ΐΒψΒΡΕΰ¥ΈΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ©«σ÷±œΏDEΒΡΫβΈω ΫΚΆΒψMΒΡΉχ±ξΘΜ
Θ®3Θ©»τΖ¥±»άΐΚ· ΐy= ![]() Θ®xΘΨ0Θ©ΒΡΆΦœσΨ≠ΙΐΒψMΘ§«σΗΟΖ¥±»άΐΚ· ΐΒΡΫβΈω ΫΘ§≤ΔΆ®ΙΐΦΤΥψ≈–ΕœΒψN «Ζώ‘ΎΗΟΚ· ΐΒΡΆΦœσ…œΘ°
Θ®xΘΨ0Θ©ΒΡΆΦœσΨ≠ΙΐΒψMΘ§«σΗΟΖ¥±»άΐΚ· ΐΒΡΫβΈω ΫΘ§≤ΔΆ®ΙΐΦΤΥψ≈–ΕœΒψN «Ζώ‘ΎΗΟΚ· ΐΒΡΆΦœσ…œΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com