
【题目】在正方形网格中,我们把,每个小正方形的顶点叫做格点,连接任意两个格点的线段叫网格线段,以网格线段为边组成的图形叫做格点图形,在下列如图所示的正方形网格中,每个小正方形的边长为1. 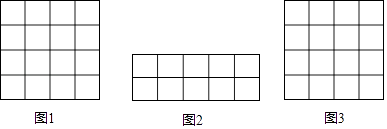
(1)请你在图1中画一个格点图形,且该图形是边长为 ![]() 的菱形;
的菱形;
(2)请你在图2中用网格线段将其切割成若干个三角形和正方形,拼接成一个与其面积相等的正方形,并在图3中画出格点正方形.
科目:初中数学 来源: 题型:
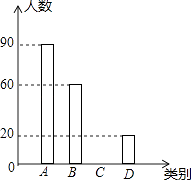
【题目】某运动品牌对第一季度A、B两款运动鞋的销售情况进行统计,两款运动鞋的销售量及总销售额如图10所示:
(1)一月份B款运动鞋的销售量是A款的![]() ,则一月份B款运动鞋销售了多少双?
,则一月份B款运动鞋销售了多少双?
(2)第一季度这两款运动鞋的销售单价保持不变,求三月份的总销售额(销售额=销售单价×销售量);
(3)结合第一季度的销售情况,请你对这两款运动鞋的进货、销售等方面提出一条建议。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=![]() 的一个交点为P(2,m),与x轴、y轴分别交于点A,B.
的一个交点为P(2,m),与x轴、y轴分别交于点A,B.
(1)求m的值
(2)若PA=2AB,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,BO、CO是角平分线.
(1)∠ABC=50°,∠ACB=60°,求∠BOC的度数,并说明理由.
(2)题(1)中,如将“∠ABC=50°,∠ACB=60°”改为“∠A=70°”,求∠BOC的度数.
(3)若∠A=n°,求∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AD 是∠A 的外角平分线,P 是 AD 上异于点 A 的任意一点,设 PB=m,PC=n,AB=c,AC=b,则 m+n_____b+c(填“>”“<”或“=”).


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康,太原市会持续出现雾霾天气吗?在2016年2月周末休息期间,某校九年级1班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计图表,观察并回答下列问题:
类别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 | m |
C | 城中村燃煤问题 | 15% |
D | 其他(绿化不足等) | n |
(1)请你求出本次被调查市民的人数及m,n的值,并补全条形统计图;
(2)若太原市有300万人口,请你估计持有A,B两类看法的市民共有多少人?
(3)学校要求小颖同学在A,B,C,D这四个雾霾天气的主要成因中,随机抽取两项作为课题研究的项目进行考察分析,请用画树状图或列表的方法,求出小颖同学刚好抽到B(汽车尾气排放),C(城中村燃煤问题)的概率.(用A,B,C,D表示各项目)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED= ![]() AB中,一定正确的是( )
AB中,一定正确的是( ) 
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,x,y满足:![]() (x-5)2+|m-2|=0,-3a2·by+1与a2b3是同类项,求整式(2x2-3xy+6y2)-m(3x2-xy+9y2)的值.
(x-5)2+|m-2|=0,-3a2·by+1与a2b3是同类项,求整式(2x2-3xy+6y2)-m(3x2-xy+9y2)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
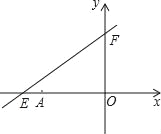
【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,且在第二象限内运动,试写出△OPA的面积S关于x的函数解析式,并写出自变量x的取值范围.
(3)探究:当点P运动到什么位置时,△OPA的面积为![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com