
如图,在平面直角坐标系中,以点M(0,3)为圆心、5为半径的圆与x轴交于点A、B(点A在点B的左侧),与y轴交于点C、D(点C在点D的上方),经过B、C两点的抛物线的顶点E在第二象限.(1)求点A、B两点的坐标.

(2)当抛物线的对称轴与⊙M相切时, 求此时抛物线的解析式.
(3)连结AE、AC、CE,若 .
.
①求点E坐标;
②在直线BC上是否存在点P,使得以点B、M、P为顶点的三角形和△ACE相似?若存在,直接写出点P的坐标;若不存在,请说明理由.
(1)(-4,0)、(4,0)
(2)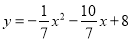
(3)①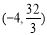 ;②
;②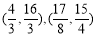
【解析】
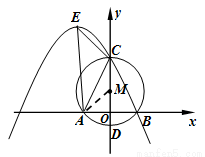
试题分析:(1)连结M A,根据勾股定理可得OA=4,所以点A的坐标是(-4,0),同理可求点B的坐标是(4,0);(2)设经过B、C两点的抛物线解析式为y=ax2+bx+c(a≠0),把点C(0,8),点B(4,0)分别代入解析式,又抛物线的对称轴与⊙M相切,所以对称轴是x=-5,解方程组便可;(3)①因为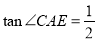 ,又在Rt△AOC中
,又在Rt△AOC中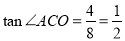 , 所以可得出AE∥CO,因此点A在抛物线的对称轴上,所以对称轴是x=-4,从而可求出二次函数解析式,可确定点E坐标,②因为根据条件可知∠CAE=∠ACO=∠BCD,因此以点B、M、P为顶点的三角形和△ACE相似时,需要分两种情况讨论.
, 所以可得出AE∥CO,因此点A在抛物线的对称轴上,所以对称轴是x=-4,从而可求出二次函数解析式,可确定点E坐标,②因为根据条件可知∠CAE=∠ACO=∠BCD,因此以点B、M、P为顶点的三角形和△ACE相似时,需要分两种情况讨论.
试题解析:(1)连结M A,由题意得:AM=5,OM=3,则OA=4,同理得OB=4,
∴点A、点B的坐标分别是(-4,0)、(4,0) 4分
(2)设经过B、C两点的抛物线解析式为y=ax2+bx+c(a≠0),把点C(0,8),点B(4,0)分别代入解析式
∴c=8,0=16a+4b+8,∴b=-4a-2;
此时,y=ax2+(-4a-2)x+8(a≠0),
它的对称轴是直线:x=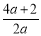 =
=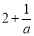 ;
;
又∵抛物线的顶点E在第二象限且该抛物线的对称轴与⊙M相切,
则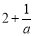 =-5,∴a=
=-5,∴a=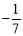 ,b=
,b=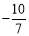 ,
,
∴抛物线的解析式为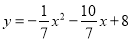 ; 8分
; 8分
(3)①在Rt△AOC中,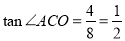 ,而
,而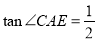 ,
,
∴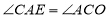 ,所以AE∥CO,即点A在抛物线的对称轴上 10分
,所以AE∥CO,即点A在抛物线的对称轴上 10分
又∵y=ax2+(-4a-2)x+8,∴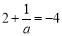 ,∴a=
,∴a=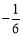 ;
;
∴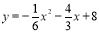
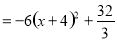
∴E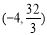 12分
12分
②在直线BC上存在点P,使得以点B、M、P为顶点的三角形和△ACE相似,
点P的坐标为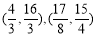 16分(每个点P的坐标各2分)
16分(每个点P的坐标各2分)
考点:1.勾股定理;2.轴对称;3.待定系数法求函数解析式;4.三角函数;5.相似三角形的判定.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源:[同步]2014年北师大版八年级上 5.4增收节支练习卷(解析版) 题型:?????
今年是祖国母亲60岁生日,小明、小敏、小新商量要在国庆前夕给祖国母亲献礼,决定画5幅国画表达大伙的爱国之情.小明说:“我来出一道数学题:把剪5幅国画的任务分配给3个人,每人至少1幅,有多少种分配方法?”小敏想了想说:“设各人的任务为x、y、z,可以列出方程x+y+z=5.”小新接着说:“那么问题就成了问这个方程有几个正整数解.”现在请你说说看:这个方程正整数解的个数是( )
A.7个 B.6个 C.5个 D.3个
查看答案和解析>>
科目:初中数学 来源:[同步]2014年北师大版八年级上 2.4估算练习卷(解析版) 题型:?????
(2014•石家庄二模)下列各数中,最大的数是( )
A.﹣1 B.2 C.0 D.
查看答案和解析>>
科目:初中数学 来源:[同步]2014年北师大版八年级上 2.4估算练习卷(解析版) 题型:?????
(2014•南京)下列无理数中,在﹣2与1之间的是( )
A.﹣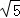 B.﹣
B.﹣ C.
C. D.
D.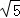
查看答案和解析>>
科目:初中数学 来源:[同步]2014年北师大版八年级上 2.4估算练习卷(解析版) 题型:?????
(2014•日照)在已知实数:﹣1,0,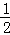 ,﹣2中,最小的一个实数是( )
,﹣2中,最小的一个实数是( )
A.﹣1 B.0 C.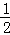 D.﹣2
D.﹣2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
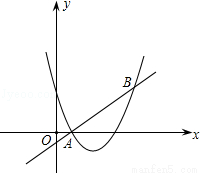
(1)求m的值和抛物线的解析式;(8分)
(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期第三次阶段性测试数学试卷(解析版) 题型:选择题
已知二次函数y=ax2+bx+c,若a<0,c>0,那么它的图象大致是( )
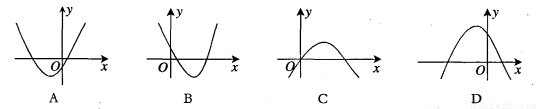
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com