
��ij�п�չ�ġ����л����䣬���������ꡱ�����»�У�Χ��ѧ�����˾��Ķ�ʱ����һ���⣬�Գ���ѧ����������������飮��ͼ�Ǹ��ݵ��������Ƴɵ�ͳ��ͼ�������������������ͼ���ṩ����Ϣ����������⣺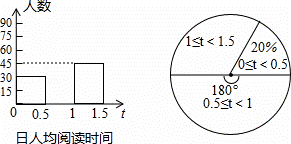
��1�����γ�����������������Ƕ��٣�
��2���뽫����ͳ��ͼ����������
��3��������ͳ��ͼ�У���������˾��Ķ�ʱ����1��1.5Сʱ��Ӧ��Բ�ĽǶ�����
��4�����ݱ��γ������飬�Թ��Ƹ���12000������ѧ�������˾��Ķ�ʱ����0.5��1.5Сʱ�Ķ����ˣ�

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
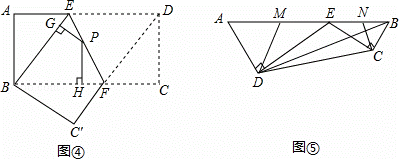
����ʦ������ѧϰ��С����С���������һ�����⣺��ͼ1���ڡ�ABC�У�AB=AC����PΪ��BC�ϵ���һ�㣬����P��PD��AB��PE��AC������ֱ�ΪD��E������C��CF��AB������ΪF����֤��PD+PE=CF��
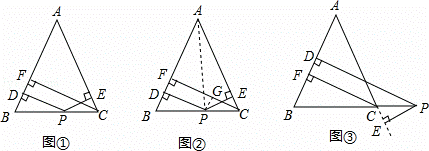
С����֤��˼·�ǣ���ͼ2������AP���ɡ�ABP���ACP���֮�͵��ڡ�ABC���������֤�ã�PD+PE=CF��
С����֤��˼·�ǣ���ͼ2������P��PG��CF������ΪG������֤�ã�PD=GF��PE=CG����PD+PE=CF��
����ʽ̽������ͼ3������P��BC�ӳ�����ʱ�������������䣬��֤��PD��PE=CF��
��������������������۵ľ���ͷ�������������⣺
���������á���ͼ4��������ABCD��EF�۵���ʹ��D���ڵ�B�ϣ���C���ڵ�C�䴦����PΪ�ۺ�EF�ϵ���һ�㣬����P��PG��BE��PH��BC������ֱ�ΪG��H����AD=8��CF=3����PG+PH��ֵ��
��Ǩ����չ��ͼ5��һ����ģ�Ľ���ʾ��ͼ�����ı���ABCD�У�EΪAB���ϵ�һ�㣬ED��AD��EC��CB������ֱ�ΪD��C����AD•CE=DE•BC��AB=2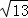 dm��AD=3dm��BD=
dm��AD=3dm��BD=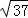 dm��M��N�ֱ�ΪAE��BE���е㣬����DM��CN�����DEM���CEN���ܳ�֮�ͣ�
dm��M��N�ֱ�ΪAE��BE���е㣬����DM��CN�����DEM���CEN���ܳ�֮�ͣ�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��M��N�����������ϱ�ʾ�����ֱ���m��n��������ʽ���г������ǣ�������
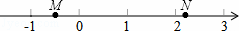
| �� | A�� | m+n��0 | B�� | ﹣m��﹣n | C�� | |m|﹣|n|��0 | D�� | 2+m��2+n |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪A��C�������40ǧ�ף�B��C�������50ǧ�ף����������ֱ��A��B����ͬʱ������C�أ����ҳ�ÿСʱ�ȼ׳�����ʻ12ǧ�ף�������ͬʱ����C�أ����ҳ����ٶ�Ϊxǧ��/Сʱ���������з�����ȷ���ǣ�������
| �� | A�� |
| B�� |
| C�� |
| D�� |
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
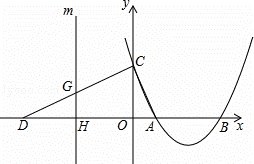
��ͼ����A��1��0����B��3��0����x��Ĵ��ߣ��ֱ�ֱ��y=4��x��C��D���㣮������y=ax2+bx+c����O��C��D���㣮
��1���������ߵı���ʽ��
��2����MΪֱ��OD�ϵ�һ�����㣬��M��x��Ĵ��߽��������ڵ�N�����Ƿ���������ĵ�M��ʹ����A��C��M��NΪ������ı���Ϊƽ���ı��Σ������ڣ����ʱ��M�ĺ����ꣻ�������ڣ���˵�����ɣ�
��3������AOC��CD����ƽ�ƣ���C���߶�CD�ϣ��Ҳ����D�غϣ�����ƽ�ƵĹ����С�AOC���OBD�ص����ֵ������ΪS������S�����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����˵����ȷ���ǣ�������
| �� | A�� | ����ε���Ǻ�������й� |
| �� | B�� | ƽ���ı��μ�����Գ�ͼ�Σ��������ĶԳ�ͼ�� |
| �� | C�� | ����Բ����ʱ��Բ�ľ������Բ�İ뾶֮�� |
| �� | D�� | �����ε��κ����ߵĺʹ��ڵ����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��������y=ax2��8ax+12a��a��0����x�ύ��A��B���㣨A��B����ࣩ����y�ύ�ڵ�C����D������Ϊ����6��0�����ҡ�ACD=90�㣮
��1����ֱ��д��A��B��������ꣻ
��2���������ߵĽ���ʽ��
��3�������ߵĶԳ������Ƿ���ڵ�P��ʹ�á�PAC���ܳ���С�������ڣ������P�����꼰�ܳ�����Сֵ���������ڣ�˵�����ɣ�
��4��ƽ����y���ֱ��m�ӵ�D������x������ƽ���ƶ�������Aֹͣ����ֱ��m������DCA�Ľ���ΪG����x��Ľ���ΪH��t��0�����ǡ�ACD��ֱ��m��ಿ�ֵ����Ϊs����s����t�ĺ�����ϵʽ���Ա���t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com