练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图①，现有一张三角形ABC纸片，沿BC边上的高AE所在的直线翻折，使得点C与BC边上的点D重合．

    （1）填空：△ADC是 三角形；

    （2）若AB=15，AC=13，BC=14，求BC边上的高AE的长；

    （3）如图②，若∠DAC=90°，试猜想：BC、BD、AE之间的数量关系，并加以证明．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2015-2016学年广东东莞樟木头中学七年级上第一次月考数学卷（解析版） 题型：计算题

    计算：．

    查看答案和解析>>

    科目：初中数学 来源：2015-2016学年广西柳州八年级下期末数学试卷（解析版） 题型：选择题

    下列计算正确的是（ ）

    A．+= B．﹣=﹣1 C．×=6 D．÷=3

    查看答案和解析>>

    科目：初中数学 来源：2015-2016学年广东深圳市南山区八年级下期末数学试卷（解析版） 题型：选择题

    △ABC为等腰直角三角形，∠ACB=90°，AC=BC=2，P为线段AB上一动点，D为BC上中点，则PC+PD的最小值为（ ）

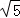    A． B．3 C． D．

    查看答案和解析>>

    科目：初中数学 来源：2015-2016学年广东深圳市南山区八年级下期末数学试卷（解析版） 题型：选择题

    要使分式有意义，那么x的取值范围是（ ）

    A．x≠3 B．x≠3且x≠﹣3 C．x≠0且x≠﹣3 D．x≠﹣3

    查看答案和解析>>

    科目：初中数学 来源：2015-2016学年福建泉州晋江市安海片区八年级上期末数学卷（解析版） 题型：解答题

    分解因式：4x3﹣4x2+x．

    查看答案和解析>>

    科目：初中数学 来源：2015-2016学年福建泉州晋江市安海片区八年级上期末数学卷（解析版） 题型：填空题

    命题“周长相等的两个三角形全等”是 命题．（填“真”或“假”）

    查看答案和解析>>

    科目：初中数学 来源：2016届湖北赤壁一中学九年级2月月考数学试卷（解析版） 题型：计算题

    计算：

    查看答案和解析>>

    科目：初中数学 来源：2016年初中毕业升学考试（天津卷）数学（解析版） 题型：解答题

    已知抛物线C：y=x2﹣2x+1的顶点为P，与y轴的交点为Q，点F（1，）．

    （Ⅰ）求点P，Q的坐标；

    （Ⅱ）将抛物线C向上平移得到抛物线C′，点Q平移后的对应点为Q′，且FQ′=OQ′．

    ①求抛物线C′的解析式；

    ②若点P关于直线Q′F的对称点为K，射线FK与抛物线C′相交于点A，求点A的坐标．

    查看答案和解析>>

    同步练习册答案