
【题目】如图,B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(0≤t≤10).
(1)当t=2时,①AB= cm.②求线段CD的长度.
(2)①点B沿点A→D运动时,AB= cm;
②点B沿点D→A运动时,AB= cm.(用含t的代数式表示AB的长)
(3)在运动过程中,若AB中点为E,则EC的长是否变化,若不变,求出EC的长;若发生变化,请说明理由.
![]()
【答案】(1)CD=3cm;(2)①2tcm;②20﹣2tcm;(3)EC=5cm.
【解析】
(1)①根据速度乘以时间等路程,可得答案;②根据线段的和差,可得BD的长,根据线段中点的性质,可得答案;
(2)①根据速度乘以时间等路程,可得答案;
②根据线段的和差,可得AB的长;
(3)根据线段中点的性质,可得BE的长,BC的长,根据线段的和差,可得答案.
解:(1)当t=2时,①AB=2×2=4cm;
②BD=AD﹣AB=10﹣4=6cm,
由C是线段BD的中点,得
CD=![]() BD=
BD=![]() ×6=3cm;
×6=3cm;
(2))①点B沿点A→D运动时,AB=2tcm;
②点B沿点D→A运动时,AB=20﹣2tcm;
(3)在运动过程中,若AB中点为E,则EC的长不变,
由AB中点为E,C是线段BD的中点,得
BE=![]() AB,BC=
AB,BC=![]() BD.
BD.
EC=BE+BC=![]() (AB+BD)=
(AB+BD)=![]() ×10=5cm.
×10=5cm.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,延长
边上一点,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 的垂直平分线于点
的垂直平分线于点![]() ,连接
,连接![]() .
.
(1)如图1,当点![]() 与点
与点![]() 重合时,证明:
重合时,证明:![]() ;
;

(2)如图2,当点![]() 不与
不与![]() ,
,![]() 两点重合时,(1)中的结论是否还成立?并说明理由.
两点重合时,(1)中的结论是否还成立?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如∠MON=30°、OP=6,点A、B分别在OM、ON上;(1)请在图中画出周长最小的△PAB(保留画图痕迹);(2)请求出(1)中△PAB的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°

(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?

(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系? (2、3小题只需选一题说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c满足|a-![]() |+
|+![]() +(c-
+(c-![]() )2=0.
)2=0.
(1)求a,b,c的值;
(2)试问以a,b,c为边能否构成三角形?若能,求出其周长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
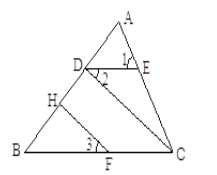
【题目】已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.
证明:∵∠1=∠ACB(已知)
∴DE∥BC( )
∴∠2= ( )
∵∠2=∠3(已知)
∴∠3=
∴CD∥FH( )
∴∠BDC=∠BHF( )
又∵FH⊥AB(已知)
∴ ( )
∵CD∥FH
∴∠BHF=∠BDC=90°( )
即CD⊥AB( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需要的时间与原计划生产450台机器所需要的时间相同.
(1)原计划平均每天生产多少台机器?
(2)若该工厂要在不超过5天的时间,生产1100台机器,则平均每天至少还要再多生产多少台机器?
查看答案和解析>>
科目:初中数学 来源: 题型:
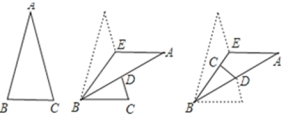
【题目】如图,△ABC中∠A=30°,E是AC边上的点,先将△ABE沿着BE翻折,翻折后△ABE的AB边交AC于点D,又将△BCD沿着BD翻折,C点恰好落在BE上,此时∠CDB=80°,则原三角形的∠B为 _____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com