
【题目】如∠MON=30°、OP=6,点A、B分别在OM、ON上;(1)请在图中画出周长最小的△PAB(保留画图痕迹);(2)请求出(1)中△PAB的周长.

【答案】(1)见解析; (2) 6.
【解析】
(1)设点P关于OM、ON对称点分别为P′、P″,当点A、B在P′P″上时,△PAB周长为PA+AB+BP=P′P″,此时周长最小.(2)根据轴对称的性质,可得△OP′P″是等边三角形即可解决问题.
(1)如图所示:
分别作点P关于OM、ON的对称点P′、P″,连接OP′、OP″、P′P″,P′P″交OM、ON于点A.B,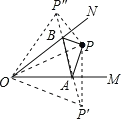
连接PA、PB,此时△PAB周长的最小值等于P′P″.
(2)如图所示:由轴对称性质可得,
OP′=OP″=OP=6cm,∠P′OA=∠POA,∠P″OB=∠POB,
所以∠P′OP″=2∠MON=2×30°=60°,
因为OP′=OP″,所以△OP″P′是等边三角形,
∴P′P″=6cm,
∴△APB的周长最小值为6cm,
故答案为6.


科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.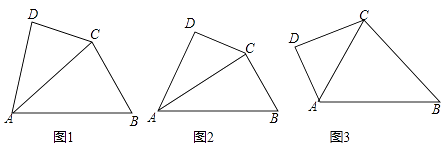
(1)如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(2)如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.
(1)轮船到达目的地开始卸货,平均卸货速度v(单位:吨/天)与卸货天数t之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上货物不超过5天卸货完毕,那么平均每天至少要缷货多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点B1、B2、B3…和A1、A2、A3…分别在OM和ON上,且△A1B1A2、△A2B2A3、△A3B3A4、…分别为等边三角形,已知OA1=1,则△A2018B2018A2019的边长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
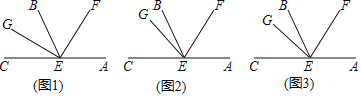
【题目】如图,E是直线AC上一点,EF是∠AEB的平分线.
(1)如图1,若EG是∠BEC的平分线,求∠GEF的度数;
(2)如图2,若GE在∠BEC内,且∠CEG=3∠BEG,∠GEF=75°,求∠BEG的度数.
(3)如图3,若GE在∠BEC内,且∠CEG=n∠BEG,∠GEF=α,求∠BEG(用含n、α的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题提出】如图①,已知海岛A到海岸公路BD的距离为AB,C为公路BD上的酒店,从海岛A到酒店C,先乘船到登陆点D,船速为a,再乘汽车,车速为船速的n倍,点D选在何处时,所用时间最短?
【特例分析】若n=2,则时间t= ![]() +
+ ![]() ,当a为定值时,问题转化为:在BC上确定一点D,使得AD+
,当a为定值时,问题转化为:在BC上确定一点D,使得AD+ ![]() 的值最小.如图②,过点C做射线CM,使得∠BCM=30°.
的值最小.如图②,过点C做射线CM,使得∠BCM=30°.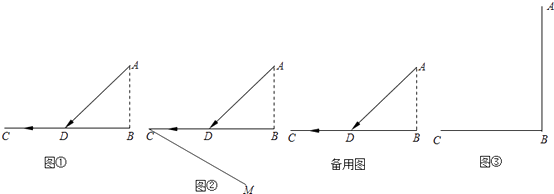
(1)过点D作DE⊥CM,垂足为E,试说明:DE= ![]() ;
;
(2)【问题解决】请在图②中画出所用时间最短的登陆点D′,并说明理由.
(3)【模型运用】请你仿照“特例分析”中的相关步骤,解决图①中的问题(写出具体方案,如相关图形呈现、图形中角所满足的条件、作图的方法等).
(4)如图③,海面上一标志A到海岸BC的距离AB=300m,BC=300m.救生员在C点处发现标志A处有人求救,
立刻前去营救,若救生员在岸上跑的速度都是6m/s,在海中游泳的速度都是2m/s,求救生员从C点出发到
达A处的最短时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1的函数关系式为![]() ,且l1与x轴交于点D,直线l2经过定点A(4,0),B(﹣1,5),直线l1与l2相交于点C,
,且l1与x轴交于点D,直线l2经过定点A(4,0),B(﹣1,5),直线l1与l2相交于点C,

(1)求直线l2的解析式;
(2)求△ADC的面积;
(3)在直线l2上存在一点F(不与C重合),使得△ADF和△ADC的面积相等,请求出F点的坐标;
(4)在x轴上是否存在一点E,使得△BCE的周长最短?若存在请求出E点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(0≤t≤10).
(1)当t=2时,①AB= cm.②求线段CD的长度.
(2)①点B沿点A→D运动时,AB= cm;
②点B沿点D→A运动时,AB= cm.(用含t的代数式表示AB的长)
(3)在运动过程中,若AB中点为E,则EC的长是否变化,若不变,求出EC的长;若发生变化,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等.无论正方形A1B1C1O绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com