
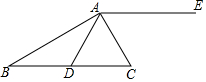
 如图,在△ABC中,点D在BC边上,BD=AD=AC,AC平分∠DAE.
如图,在△ABC中,点D在BC边上,BD=AD=AC,AC平分∠DAE.分析 (1)根据AC平分∠DAE,可得∠DAC=∠CAE=x°,将△ADC绕点A逆时针旋转x°,则点C'落在AE上,根据AD=AC,可得点D落在点C处;
(2)先判定△ADC是等边三角形,得出AD=AC=DC,由(1)得,A C′=AC,CC′=DC,据此可得AD=DC=CC′=A C′.
解答 解:(1)如图所示.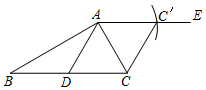
(2)证明:∵BD=AD,
∴∠B=∠BAD=30°.
∴∠ADC=∠B+∠BAD=60°.
∵AD=AC,
∴△ADC是等边三角形.
∴AD=AC=DC.
由(1)得,AC′=AC,CC′=DC,
∴AD=DC=CC′=A C′.
∴四边形ADCC′是菱形.
点评 本题主要考查了菱形的判定以及旋转变换,解题时注意:四条边都相等的四边形是菱形.


科目:初中数学 来源: 题型:选择题
| 诗词数量(首) | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 人数 | 3 | 4 | 4 | 5 | 7 | 5 | 1 | 1 |
| A. | 11,7 | B. | 7,5 | C. | 8,8 | D. | 8,7 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
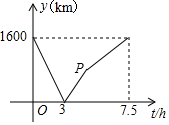 【情景】A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),相距y(km)与时间t(h)满足的数量关系如图所示.
【情景】A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),相距y(km)与时间t(h)满足的数量关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
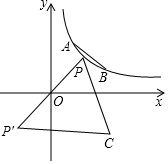 如图点A(1,2)、B(2,1)在反比例函数y=$\frac{2}{x}$图象上,点P是反比例函数y=$\frac{2}{x}$在第一象限图象上的一个动点,作点P关于原点对称的点P′,以P P′为边作等边△P P′C,点C(x,y)在第四象限.
如图点A(1,2)、B(2,1)在反比例函数y=$\frac{2}{x}$图象上,点P是反比例函数y=$\frac{2}{x}$在第一象限图象上的一个动点,作点P关于原点对称的点P′,以P P′为边作等边△P P′C,点C(x,y)在第四象限.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知?ABCD.
如图,已知?ABCD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
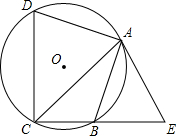 如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.
如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com