
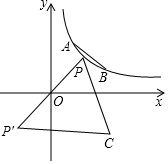
 如图点A(1,2)、B(2,1)在反比例函数y=$\frac{2}{x}$图象上,点P是反比例函数y=$\frac{2}{x}$在第一象限图象上的一个动点,作点P关于原点对称的点P′,以P P′为边作等边△P P′C,点C(x,y)在第四象限.
如图点A(1,2)、B(2,1)在反比例函数y=$\frac{2}{x}$图象上,点P是反比例函数y=$\frac{2}{x}$在第一象限图象上的一个动点,作点P关于原点对称的点P′,以P P′为边作等边△P P′C,点C(x,y)在第四象限.分析 (1)如图1中,作PE⊥y轴于E,CF⊥x轴于F,连接OC,设P(m,n).首先证明C($\sqrt{3}$n,-$\sqrt{3}$m),点C在反比例函数y=-$\frac{6}{x}$上(x>0);
(2)利用(1)中结论,分两种情形讨论即可解决问题.
解答 解:(1)如图1中,作PE⊥y轴于E,CF⊥x轴于F,连接OC,设P(m,n).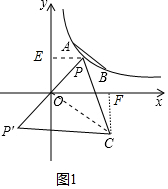
易证△POE∽△COF,
∴$\frac{OP}{OC}$=$\frac{PE}{CF}$=$\frac{OE}{OF}$=$\frac{1}{\sqrt{3}}$,
∴CF=$\sqrt{3}$n,OF=$\sqrt{3}$m,
∴C($\sqrt{3}$n,-$\sqrt{3}$m),
∵mn=2,
∴$\sqrt{3}$n•(-$\sqrt{3}$m)=-3mn=-6,
∴点C在反比例函数y=-$\frac{6}{x}$上(x>0),
当P与A重合时,C(2$\sqrt{3}$,-$\sqrt{3}$),
故答案为(2$\sqrt{3}$,-$\sqrt{3}$).
(2)如图2中,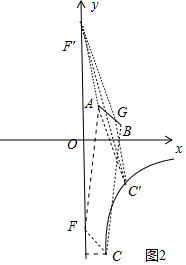
观察图象可知:当CF为边时,G与B重合,CF=AB=$\sqrt{2}$,此时C(1,-6),
∴y≤-6时,存在以A、G、F、C这样的四个点为顶点的四边形是平行四边形,
当CF为对角线时,G与B重合时,易证C′(3,-2),G与A重合时,A是C′F′的中点,此时C(2,-3),
观察图象可知当-3<y≤-2时,存在以A、G、F、C这样的四个点为顶点的四边形是平行四边形,
综上所述,满足条件的y的取值范围为y≤-6或-3<y≤-2.
故答案为y≤-6或-3<y≤-2.
点评 本题考查反比例函数的应用,平行四边形的判定和性质、全等三角形的判定和性质,相似三角形的判定和性质等知识,综合性比较强,属于中考填空题中的压轴题.


科目:初中数学 来源: 题型:选择题
| A. | 7.2×106 | B. | 72×106 | C. | 7.2×107 | D. | 0.72×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价(元/个) | 100 | 110 | 120 | 130 | … |
| 月销量(个) | 200 | 180 | 160 | 140 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
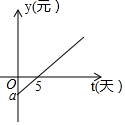 某地蔬菜市场采用如下经营模式:个体蔬菜经营商向市场管理部门租赁摊位,每月缴纳一定的“摊位费”(含市场管理等费用),蔬菜市场管理公司靠收每户的“摊位费”盈利,个体经营商每经营一天,平均可得“营业额”800元,但平均每天要支付蔬菜的“进货费”400元,如图是某个体蔬菜经营商经营一个月(均按30天计算)的收益(除去“摊位费”和“进货费”)y元随经营时间t天变化的函数图象.
某地蔬菜市场采用如下经营模式:个体蔬菜经营商向市场管理部门租赁摊位,每月缴纳一定的“摊位费”(含市场管理等费用),蔬菜市场管理公司靠收每户的“摊位费”盈利,个体经营商每经营一天,平均可得“营业额”800元,但平均每天要支付蔬菜的“进货费”400元,如图是某个体蔬菜经营商经营一个月(均按30天计算)的收益(除去“摊位费”和“进货费”)y元随经营时间t天变化的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
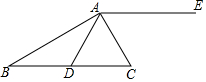 如图,在△ABC中,点D在BC边上,BD=AD=AC,AC平分∠DAE.
如图,在△ABC中,点D在BC边上,BD=AD=AC,AC平分∠DAE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
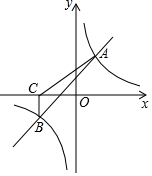 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com