

分析 (1)设⊙O的半径为r,利用MP=NP=AP=BP=r可计算出$\frac{{MP}^{2}+{NP}^{2}}{{AB}^{2}}$=$\frac{1}{2}$;
(2)如图2,作OH⊥MN于H,连接ON,根据垂径定理得到MP=NP=$\frac{1}{2}$MN=4,则PH=3,再根据等腰直角三角形的性质得OH=PH=3,接着根据勾股定理计算出ON=5,然后计算$\frac{{MP}^{2}+{NP}^{2}}{{AB}^{2}}$的值;
(3)作OH⊥MN于H,连接OM,如图2,设PM=a,PN=b,根据垂径定理得到MP=NP=$\frac{a+b}{2}$,则PH=$\frac{a-b}{2}$,再根据等腰直角三角形的性质得OH=PH=$\frac{a-b}{2}$,接着根据勾股定理计算出OM=$\sqrt{ab}$,然后计算$\frac{{MP}^{2}+{NP}^{2}}{{AB}^{2}}$的中可得到$\frac{{MP}^{2}+{NP}^{2}}{{AB}^{2}}$=$\frac{1}{2}$.
解答 解:(1)设⊙O的半径为r,
∵点P与圆心O重合,
∴MP=NP=AP=BP=r,
∴$\frac{{MP}^{2}+{NP}^{2}}{{AB}^{2}}$=$\frac{{r}^{2}+{r}^{2}}{4{r}^{2}}$=$\frac{1}{2}$;
(2)如图2,作OH⊥MN于H,连接ON,
∴MP=NP=$\frac{1}{2}$MN=4,
∴PH=MH-MP=4-1=3,
∵∠NPB=45°,
∴OH=PH=3,
在Rt△PON中,ON=$\sqrt{O{H}^{2}+N{H}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴$\frac{{MP}^{2}+{NP}^{2}}{{AB}^{2}}$=$\frac{{1}^{2}+{7}^{2}}{1{0}^{2}}$=$\frac{1}{2}$;
(3)(2)中结论不改变.
作OH⊥MN于H,连接OM,如图2,设PM=a,PN=b,
∴MP=NP=$\frac{a+b}{2}$,
∴PH=NH-PN=$\frac{a-b}{2}$,
∵∠NPB=45°,
∴∠OPH=45°,
∴OH=PH=$\frac{a-b}{2}$,
在Rt△OMH中,OM=$\sqrt{O{H}^{2}+M{H}^{2}}$=$\sqrt{(\frac{a+b}{2})^{2}+(\frac{a-b}{2})^{2}}$=$\sqrt{ab}$,
∴$\frac{{MP}^{2}+{NP}^{2}}{{AB}^{2}}$=$\frac{{a}^{2}+{b}^{2}}{(2\sqrt{\frac{{a}^{2}+{b}^{2}}{2}})^{2}}$=$\frac{1}{2}$.
点评 本题考查了圆的综合题:熟练掌握垂径定理和等腰直角三角形的性质;会运用勾股定理计算线段的长.过圆心作弦的垂线是常作的辅助线.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AD是∠BAC的平分线,DE⊥AC于点E,DM=DN,若△AMD的面积为100,△AND的面积为80;则△DEN的面积为10.
如图,在△ABC中,AD是∠BAC的平分线,DE⊥AC于点E,DM=DN,若△AMD的面积为100,△AND的面积为80;则△DEN的面积为10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
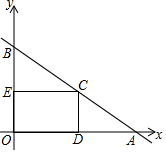 如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(6,0),B(0,3)两点,点C为线段AB上的一动点,过点C作CD⊥x轴于点D.
如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(6,0),B(0,3)两点,点C为线段AB上的一动点,过点C作CD⊥x轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
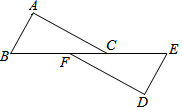 如图,△ABC≌△DEF,则下列结论中,成立的有①②③④.(填序号)
如图,△ABC≌△DEF,则下列结论中,成立的有①②③④.(填序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com