
����Ŀ����һ����20cm����˿�������Σ�����ÿһ����˿�ij���Ϊ�ܳ�������һ�������Σ�������һ����˿��Ϊ4x cm�����������ε������Ϊy cm2
��1����y��x�ĺ�����ϵʽ��
��2��Ҫʹ���������������֮��Ϊ17cm2����ô�����˿�������κ�ij��ȷֱ��Ƕ��٣�
��3��Ҫʹ���������������֮����С���������˿�������κ�ij��ȸ��Ƕ��٣����������������֮����СΪ���٣�
���𰸡���1��y=2x2��10x+25����2��4cm��16cm����3���������ξ�Ϊ10cm�ij���ʱ���֮����С����С�����Ϊ12.5cm2��
��������
�����������1���������֪��������һ�γ�Ϊ4xcm������һ�γ�Ϊ20��4xcm������������������ܳ���ת����ϵ�������ε����=![]() ���ܳ����ܳ����г�����ĺ�����ϵʽ��
���ܳ����ܳ����г�����ĺ�����ϵʽ��
��2����y=17ʱ���з��̼��ɵõ����ۣ�
��3�����ݺ��������������ֵ��
�⣺��1����һ����˿�ij���Ϊ4x����һ��Ϊ��20��4x������߳��ֱ�Ϊx��![]() ��20��4x��=5��x��
��20��4x��=5��x��
��y=x2+��5��x����5��x��=2x2��10x+25��
��2��1��y=17ʱ��
��2x2��10x+25=17��
��ã�x=1����x=4��
�������˿�������κ�ij��ȷֱ���4cm��16cm��
��3����y=2x2��10x+25=2��x��![]() ��2+12.5��
��2+12.5��
���������ξ�Ϊ10cm�ij���ʱ���֮����С����С�����Ϊ12.5cm2��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����1+��2=180����A=��C��DAƽ�֡�BDF��
��1����֤��AE��FC.
��2��AD��BC��λ�ù�ϵ��Σ�Ϊʲô��
��3��֤����BCƽ�֡�DBE.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������m����ʾ�ĵ㵽��3����4����λ��a��b��Ϊ�෴�����Ҷ���Ϊ�㣬c��d��Ϊ����.�� ![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OΪԲ�ĵ�����ͬ��Բ����Բ�뾶Ϊ5��СԲ�뾶Ϊ![]() ����PΪ��Բ�ϵ�һ�㣬PC��PB��СԲ�ڵ�A����B������Բ��C��D���㣬��EΪ��CD����һ�㣬��AE+OE����СֵΪ ��
����PΪ��Բ�ϵ�һ�㣬PC��PB��СԲ�ڵ�A����B������Բ��C��D���㣬��EΪ��CD����һ�㣬��AE+OE����СֵΪ ��
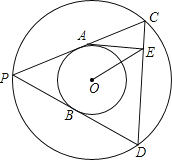
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E��ֱ��DF�ϣ���B��ֱ��AC�ϣ�����1����2����3����4������A����F����˵�����ɣ�
�⣺�ߡ�1����2����֪������2����DGF�� ��
���1����DGF
��BD��CE�� ��
���3����C��180�� ��
���ߡ�3����4����֪��
���4����C��180
��_______��_________ ��ͬ���ڽǻ�������ֱ��ƽ�У�
���A����F�� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=2x2+3��������A��x1 �� y1����B��x2 �� y2������x1��x2 �� y1=y2 �� ��x=x1+x2ʱ��y= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʹ����ֱ��������ȫ�ȵ������ǣ� ��
A. б�ߡ�ֱ�DZ߶�Ӧ���
B. ��ֱ�DZ߶�Ӧ���
C. һ��Ǻ�б�߶�Ӧ���
D. ����Ƕ�Ӧ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������һ������2��A�ͳ���1��B�ͳ�װ��ˮ����һ���˻�10�֣��ڶ�������1��A�ͳ���2��B�ͳ�װˮ����һ���˻�11�֣������˻��������أ�
����ÿ��A�ͳ���B�ͳ�����ʱ��װˮ�����ٶ֣�
������31��ˮ�����˳����ƻ�ͬʱ����A�ͳ���B�ͳ�һ�����꣬��ÿ������ǡ��װ��������Ƴ����ļ����������
����A�ͳ�ÿ�����200Ԫ��B�ͳ�ÿ�����300Ԫ���������������ʡǮ����ʡǮ�ķ����ܹ�������Ǯ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2015��4��8�գ��㶫ʡ��ƶ������յ���88�Ұ�����ҵ�ϼ�217000000Ԫ�ľ�������217000000�ÿ�ѧ��������ʾΪ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com