Question

19．已知如图1，二次函数y=ax²+4ax+$\frac{3}{4}$的图象交x轴于A、B两点（A在B的左侧），过A点的直线y=kx+3k（k$＞\frac{1}{4}$）交该二次函数的图象于另一点C（x₁，y₁），交y轴于M．
（1）直接写出A点坐标，并求该二次函数的解析式；
（2）过点B作BD⊥AC交AC于D，若M（0，3$\sqrt{3}$）且点Q是线段DC上的一个动点，求出当△DBQ与△AOM相似时点Q的坐标；
（3）设P（-1，-2），图2中连CP交二次函数的图象于另一点E（x₂，y₂），连AE交y轴于N，请你探究OM•ON的值的变化情况，若变化，求其变化范围；若不变，求其值．

Answer 1

分析 （1）由直线y=kx+3k（k＞$\frac{1}{4}$）过点A，可求出点A的坐标，然后把点A的坐标代入y=ax²+4ax+$\frac{3}{4}$，可求出a的值；
（2）根据有两个角相等的三角形相似，可得①∠DQB=∠OMA，②∠DQB=∠A．①根据平行线的判定与性质，可得Q点的横坐标，根据自变量与函数值的对应关系，可得答案；②根据等腰三角形的判定，可得关于m的方程，根据解方程，可得m的值，再根据自变量与函数值的对应关系，可得答案；
（3）直线PC解析式为y=ax+a-2，与抛物线y=$\frac{1}{4}$x²+x+$\frac{3}{4}$联立得到关于x的一元二次方程，由根与系数的关系知x₁+x₂=4a-4，x₁x₂=11-4a，根据$\frac{OM}{OA}$$•\frac{ON}{OA}$=$\frac{{y}_{1}}{{x}_{1}-{x}_{A}}$•$\frac{{y}_{2}}{{x}_{2}-{x}_{A}}$得到OM•ON=$\frac{1}{2}$OA²，得到结果为定值

解答 解：（1）∵直线y=kx+3k（k＞$\frac{1}{4}$）过点A，
∴y=0时，0=kx+3k，
解得：x=-3，
∴A（-3，0），
把点A的坐标代入y=ax²+4ax+$\frac{3}{4}$，得
9a-12a+$\frac{3}{4}$=0，
解得：a=$\frac{1}{4}$，
抛物线的解析式为y=$\frac{1}{4}$x²+x+$\frac{3}{4}$；
（2）如图1，，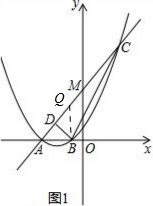
当y=0时，$\frac{1}{4}$x²+x+$\frac{3}{4}$=0，解得x=-3，x=-1，即A（-3，0），B（-1，0）．
设AM的解析式为y=kx+b，将A、M点的坐标代入，得
AM的解析式为y=$\sqrt{3}$x+3$\sqrt{3}$．
①当∠DQB=∠OMA时，QB∥OM，Q点的横坐标等于B点的横坐标-1，
当x=-1时，y=2$\sqrt{3}$，即Q（-1，2$\sqrt{3}$）；
②当∠DQB=∠A时，设Q点的坐标为（m，$\sqrt{3}$m+3$\sqrt{3}$）．
AB=BQ，即（m+1）²+（$\sqrt{3}$m+3$\sqrt{3}$）²=4，化简得m²+5m+6=0．
解得m=-2，m=-3（不符合题意，舍），
当m=-2时，$\sqrt{3}$m+3$\sqrt{3}$=$\sqrt{3}$，即Q（-2，$\sqrt{3}$），
综上所述：当△DBQ与△AOM相似时点Q的坐标（-1，2$\sqrt{3}$），（-2，$\sqrt{3}$）；
（3）直线PC解析式为y=ax+a-2，与抛物线y=$\frac{1}{4}$x²+x+$\frac{3}{4}$联立消去y得：x²-4（a-1）x+11-4a=0，
∴x₁+x₂=4a-4，x₁x₂=11-4a，
∵$\frac{OM}{OA}$$•\frac{ON}{OA}$=$\frac{{y}_{1}}{{x}_{1}-{x}_{A}}$•$\frac{{y}_{2}}{{x}_{2}-{x}_{A}}$
=$\frac{\frac{1}{4}（{x}_{1}+1）（{x}_{1}+3）×\frac{1}{4}（{x}_{2}+1）（{x}_{2}+3）}{（{x}_{1}+3）（{x}_{2}+3）}$
=$\frac{1}{16}$（x₁+1）（x₂+1）
=$\frac{1}{16}$（11-4a+4a-4+1）
=$\frac{1}{2}$，
∴OM•ON=$\frac{1}{2}$OA²=$\frac{9}{2}$．

点评 本题主要考查了二次函数的综合题型，二次函数与三角形相似以及一元二次方程等知识的综合运用，熟练的运用数形结合是解决问题的关键．