���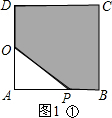
�⣺��1����������ABCD�ı߳�Ϊ12����S
������ABCD=12
2=144��
��O��AD���е㣬��OA=OD=6��
�٣���t=4ʱ����ͼ1�٣�
��AP=2��4=8��OA=6��
��S
��OAP=
��AP��OA=24��
��y=S
������ABCD-S
��OAP=144-24=120��
����t=8ʱ����ͼ1�ڣ�
��AB+BP=2��8=16��AB=12��
��BP=4����CP=12-4=8��
��y=
��OD+CP����CD=
����6+8����12=84��
����t=14ʱ����ͼ1�ۣ�

��AB+BC+CP=2��14=28��AB=BC=CD=12��
��DP=12��3-28=8��
��y=S
��ODP=
��DP��OD=24��
�ڷ����������
����0��t��6ʱ����P�ڱ�AB�ϣ���ͼ1�٣�
��AP=2t��OA=6��
��S
��OAP=
��AP��6=6t��
��y=S
������ABCD-S
��OAP=144-6t��
����6��t��12ʱ����P�ڱ�BC�ϣ���ͼ1�ڣ�
��AB+BP=2t��AB=CD=12��
��CP=24-2t��
��y=
��OD+CP����CD=
����6+24-2t����12=180-12t��
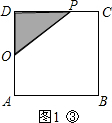
����12��t��18ʱ����P�ڱ�CD�ϣ���ͼ1�ۣ�
��AB+BC+CP=2t��AB=BC=CD=12��
��DP=36-2t��
��y=S
��ODP=
��DP��OD=108-6t��
���Ͽ�֪��y=
| | 144-6t(0��t��6) | | 180-12t(6��t��12) | | 108-6t(12��t��18) |
| |
��
��2���١�t=0ʱ��S=S
������ABCD=16��
��������ABCD�ı߳�=4��
��t=4ʱ��S=0��
��P��Q�����ڵ�4��������
�ڡ�S��t�ĺ���ͼ����5����ɣ�
��P��Q������C�㣬
��ʱ����ͬʱ���ٶ�֮�ȵ���·��֮�ȣ�����P�˶���·��=��Q�˶���·�̵�2����
���P���ٶ�=��Q���ٶȵ�2����
���Q���ٶ�Ϊa��λ����/�룬���P���ٶ�Ϊ2a��λ����/�룮
��t=4ʱ��P��Q������C�㣬������ABCD�ı߳�Ϊ4��
��4��a+2a��=4��3��
��a=1��

�ʵ�P���ٶ�Ϊ2��λ����/�룬��Q���ٶ�Ϊ1��λ����/�룻
�ۡ�������ABCD�ı߳�Ϊ4����S
������ABCD=16��
��O��AD���е㣬��OA=OD=2��
��t��ʱ��������ABCD���POQ��������Ե���ڲ����ص����ֵ����S����9��
����������������ۣ�
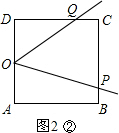
����0��t��2ʱ����P�ڱ�AB�ϣ���Q�ڱ�CD�ϣ���ͼ2�٣�
��AP=2t��DQ=t��OA=OD=2��
��S=S
������ABCD-S
��OAP-S
��ODQ=16-2t-t=16-3t��
��16-3t=9��
���t=
���������⣬��ȥ����
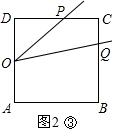
����2��t��4ʱ����P�ڱ�BC�ϣ���Q�ڱ�CD�ϣ���ͼ2�ڣ�
��AB+BP=2t��AB=4����BP=2t-4��
��DQ=t��OA=OD=2��
��S=S
������ABCD-S
����OABP-S
��ODQ=16-
����2t-4+2����4-
��2t=20-5t��
��20-5t=9��
���t=
��
����4��t��6ʱ����P�ڱ�CD�ϣ���Q�ڱ�CB�ϣ���ͼ2�ۣ�
��AB+BC+CP=2t��AB=BC=CD=4����DP=12-2t��
��DC+CQ=t����BQ=8-t��
��S=S
������ABCD-S
����OABQ-S
��ODP=16-
����2+8-t����4-
��2����12-2t��=4t-16��
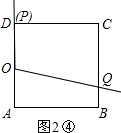
��4t-16=9��
���t=
���������⣬��ȥ����
��������6��t��8ʱ����P��D���غϣ���Q�ڱ�CB�ϣ���ͼ2�ܣ�
��DC+CQ=t��DC=4����CQ=t-4��
��S=S
����ODCQ=
����t-4+2����4=2t-4��
��2t-4=9��
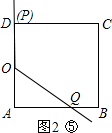
���t=
��
��������8��t��12ʱ����P��D���غϣ���Q�ڱ�AB�ϣ���ͼ2�ݣ�
��DC+CB+BQ=t��DC=CB=AB=4����AQ=12-t��
��S=S
������ABCD-S
��OAQ=16-
��2����12-t��=4+t��
��4+t=9��
���t=5���������⣬��ȥ����
���Ͽ�֪����tΪ
��
ʱ���ص��������S����9��
�ʴ�Ϊ����2����4��4����2��1��


 �⣺��1����������ABCD�ı߳�Ϊ12����S������ABCD=122=144��
�⣺��1����������ABCD�ı߳�Ϊ12����S������ABCD=122=144�� ��AB+BC+CP=2��14=28��AB=BC=CD=12��
��AB+BC+CP=2��14=28��AB=BC=CD=12�� ����12��t��18ʱ����P�ڱ�CD�ϣ���ͼ1�ۣ�
����12��t��18ʱ����P�ڱ�CD�ϣ���ͼ1�ۣ� �ʵ�P���ٶ�Ϊ2��λ����/�룬��Q���ٶ�Ϊ1��λ����/�룻
�ʵ�P���ٶ�Ϊ2��λ����/�룬��Q���ٶ�Ϊ1��λ����/�룻 ��16-3t=9��
��16-3t=9�� ��20-5t=9��
��20-5t=9�� ��4t-16=9��
��4t-16=9�� ���t=
���t=



 ��2012•����һģ����֪����ͼ��Rt��ABC�����ڡ�O���е�ֱ�ΪE��F��H����ABC=90�㣬ֱ��FE��CB����D�㣬����AO��HE�������н��ۣ�
��2012•����һģ����֪����ͼ��Rt��ABC�����ڡ�O���е�ֱ�ΪE��F��H����ABC=90�㣬ֱ��FE��CB����D�㣬����AO��HE�������н��ۣ�