
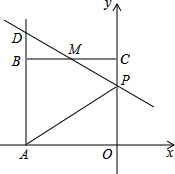
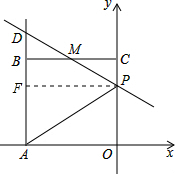
 如图,已知正方形OABC的边长为2,顶点A、C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.
如图,已知正方形OABC的边长为2,顶点A、C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 3 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |


科目:初中数学 来源: 题型:
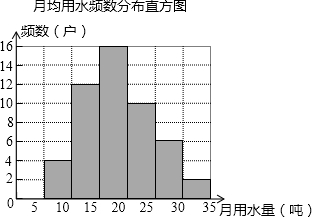 每年的3月22日被联合国为世界水日,旨在唤起公众的水意识,加强水资源保护.为响应号召,小聪同学随机调查了某小区部分家庭月均用水量并将调查数据进行整理,绘制频数分布直方图如图,则被抽查的用户中月均用水落在20~25(吨)的频率是( )
每年的3月22日被联合国为世界水日,旨在唤起公众的水意识,加强水资源保护.为响应号召,小聪同学随机调查了某小区部分家庭月均用水量并将调查数据进行整理,绘制频数分布直方图如图,则被抽查的用户中月均用水落在20~25(吨)的频率是( )| A、0.12 | B、0.2 |
| C、0.24 | D、0.32 |
查看答案和解析>>
科目:初中数学 来源: 题型:
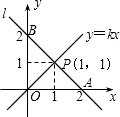 如图,在平面直角坐标系中,一条直线l:y=mx+b与x轴相交于点A(2,0),与y轴交于点B,与正比例函数y=kx(k≠0,为常数)的图象相交于点P(1,1)
如图,在平面直角坐标系中,一条直线l:y=mx+b与x轴相交于点A(2,0),与y轴交于点B,与正比例函数y=kx(k≠0,为常数)的图象相交于点P(1,1)查看答案和解析>>
科目:初中数学 来源: 题型:
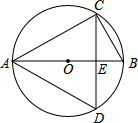 如图,在⊙O中,AB为⊙O的直径,C、D为⊙O上两点,弦AC=2
如图,在⊙O中,AB为⊙O的直径,C、D为⊙O上两点,弦AC=2| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
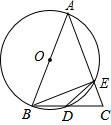 已知,如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.
已知,如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.| 2 |
 |
| BD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com