
| A. | 12-4k | B. | 6 | C. | -6 | D. | 4k-12 |
科目:初中数学 来源: 题型:解答题
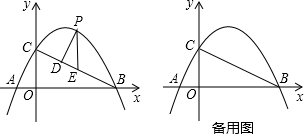
 小明和小颖在如图所示的四边形场地上,沿边骑自行车进行场地追逐赛(两人只要有一个人回到自己的出发点,则比赛结束).小明从A地出发,沿A→B→C→D→A的路线匀速骑行,速度为8米/秒;小颖从B地出发,沿B→C→D→A→B的路线匀速骑行,速度为6米/秒.已知∠ABC=90°,AB=40米,BC=80米,CD=90米.设骑行时间为t秒,假定他们同时出发且每转一个弯需要额外耗时2秒.
小明和小颖在如图所示的四边形场地上,沿边骑自行车进行场地追逐赛(两人只要有一个人回到自己的出发点,则比赛结束).小明从A地出发,沿A→B→C→D→A的路线匀速骑行,速度为8米/秒;小颖从B地出发,沿B→C→D→A→B的路线匀速骑行,速度为6米/秒.已知∠ABC=90°,AB=40米,BC=80米,CD=90米.设骑行时间为t秒,假定他们同时出发且每转一个弯需要额外耗时2秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数是14 | B. | 众数是10 | C. | 中位数是15 | D. | 方差是22 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 80+0.5x=30 | B. | 0.5x-80=30 | C. | $\frac{80}{x}$-0.5=$\frac{30}{x}$ | D. | $\frac{x}{80}$+0.5=$\frac{x}{30}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
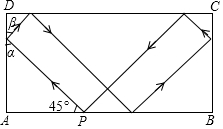 如图,击打台球时小球反弹前后的运动路线遵循对称原理,即小球反弹前后的运动路线与台球案边缘的夹角相等(α=β),在一次击打台球时,把位于点P处的小球沿所示方向击出,小球经过5次反弹后正好回到点P,若台球案的边AD的长度为4,则小球从P点被击出到回到点P,运动的总路程为( )
如图,击打台球时小球反弹前后的运动路线遵循对称原理,即小球反弹前后的运动路线与台球案边缘的夹角相等(α=β),在一次击打台球时,把位于点P处的小球沿所示方向击出,小球经过5次反弹后正好回到点P,若台球案的边AD的长度为4,则小球从P点被击出到回到点P,运动的总路程为( )| A. | 16 | B. | 16$\sqrt{2}$ | C. | 20 | D. | 20$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com