
【题目】(10分)在菱形ABCD中,E,F分别是BC,CD上的点,且CE=CF
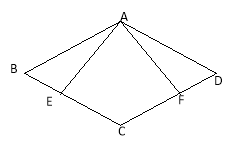
(1)求证:△ABE≌△ADF
(2)过点C作CG‖EA交AF于点H,交AD于点G,若∠BAE=25°,∠BCD=130°,求∠AHC
的度数。
【答案】(1)∵菱形ABCD,∴AB=CD,BC=AD, ∠B=∠D。又∵CE=CF, ∴BE=DF
∴△ABE≌△ADF。 (2)∠AHC=100°
【解析】
试题分析:(1)根据菱形的性质,可以得出如下
∵菱形ABCD,∴AB=CD,BC=AD, ∠B=∠D
又∵CE=CF, ∴BE=DF
根据全等三角形的判定,边角边
∴△ABE≌△ADF
(2)如图:
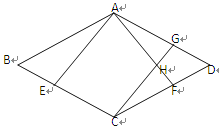
根据菱形的性质
∵∠BCD=130°, ∴∠BAD=130°, ∵∠BAE=∠DAF=25°,
∴∠EAF=130°-50°=80°
根据平行线的性质
又∵CG∥AE, ∠EAH=∠AHG
∴∠AHC=180°-∠EAH=180°-80°=100°


科目:初中数学 来源: 题型:
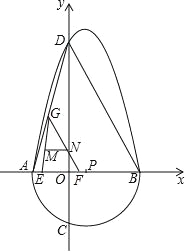
【题目】我们把一个半圆与抛物线的一部分合成的封闭图形称为“果圆”.如图,A,B,C,D是“果圆”与坐标轴的交点,点D的坐标为(0,8),且AB=6,点P是以AB为直径的半圆的圆心,P的坐标为(1,0),连接DB,AD,动点E,F分别从A,O两点出发,以相同的速度沿x轴正方向运动,当F到达B点时两点同时停止,过点F作FG∥BD交AD于点G.
(1)求“果圆”抛物线部分的解析式,并写出自变量的取值范围;
(2)在“果圆”上是否存在一点H,使得△DBH为直角三角形?若存在,求出H点的坐标;若不存在,说明理由;
(3)设M,N分别是GE,GF的中点,求在整个运动过程中,MN所扫过的图形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某招聘考试分笔试和面试两种,其中笔试按60%、面试按40%计算加权平均数,作为总成绩.孔明笔试成绩90分,面试成绩85分,那么孔明的总成绩是____分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:
我市交通有关部门规定:出租车起步价允许行驶的最远路程为2千米,超过2千米的部分按每千米另收费.甲说:“我乘这种出租车走了11千米,表上显示要付费19.2元”;乙说:“我乘这种出租车走了20千米,表上显示要付费35.4元”.请你算一算这种出租车的起步价是多少元?以及超过2千米后每千米的车费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在直线AB上,OD是∠AOC的平分线,OE是∠COB的平分线. 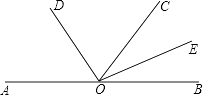
(1)求∠DOE的度数;
(2)如果∠AOD=51°17′,求∠BOE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com