
【题目】如图,点O在直线AB上,OD是∠AOC的平分线,OE是∠COB的平分线. 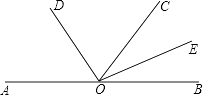
(1)求∠DOE的度数;
(2)如果∠AOD=51°17′,求∠BOE的度数.
【答案】
(1)解:∵∠AOC+∠COB=180°,已知OD是∠AOC的平分线,OE是∠COB的平分线,
∴∠DOC= ![]() ∠AOC,∠COE=
∠AOC,∠COE= ![]() ∠COB,
∠COB,
∴∠DOE=∠DOC+∠COE= ![]() (∠AOC+∠COB)=90°
(∠AOC+∠COB)=90°
(2)解:∵∠AOD+∠BOE=90°,∠AOD=51°17′,
∴∠BOE=90°﹣∠AOD=38°43′.
故答案为90°、38°43′
【解析】(1)由∠AOC+∠COB=180°,又知OD是∠AOC的平分线,OE是∠COB的平分线,故知∠DOE=∠DOC+∠COE= ![]() (∠AOC+∠COB),(2)由∠AOD+∠BOE=90°和∠AOD=51°17′,故能得到∠BOE的度数.
(∠AOC+∠COB),(2)由∠AOD+∠BOE=90°和∠AOD=51°17′,故能得到∠BOE的度数.
【考点精析】本题主要考查了角的平分线和角的运算的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示才能正确解答此题.


科目:初中数学 来源: 题型:
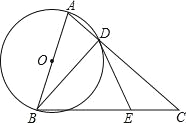
【题目】如图,在△ABC中,AC=BC,以AB为直径的⊙O交AC边于点D,点E在BC上,连结BD,DE,∠CDE=∠ABD.
(1)证明:DE是⊙O的切线;
(2)若BD=12,sin∠CDE=![]() ,求圆O的半径和AC的长.
,求圆O的半径和AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在菱形ABCD中,E,F分别是BC,CD上的点,且CE=CF
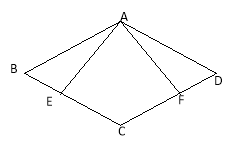
(1)求证:△ABE≌△ADF
(2)过点C作CG‖EA交AF于点H,交AD于点G,若∠BAE=25°,∠BCD=130°,求∠AHC
的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c为△ABC三边长,且满足a2c2-b2c2=a4-b4,则它的形状为( )
A. 直角三角形 B. 等腰三角形 C. 等腰直角三角形 D. 等腰三角形或直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台风是一种自然灾害,它以台风中心为圆心,在周围数千米范围内形成气旋风暴,有极强的破坏力.根据气象观测,距沿海某城市A的正南方向220 km的B处有一台风中心,其中心最大风力为12级,每远离台风中心20 km,风力就会减弱一级.该台风中心正以15 km/h的速度沿北偏东30°方向往C处移动,且台风中心风力不变.若城市所受风力达到或超过四级,则称受台风影响.该城市是否受到该台风的影响?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
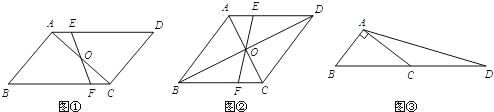
【题目】猜想:如图①,在ABCD中,点O是对角线AC的中点,过点O的直线分别交AD、BC于点E、F.若ABCD的面积是10,则四边形CDEF的面积是 .
探究:如图②,在菱形ABCD中,对角线AC、BD相交于点O,过点O的直线分别交AD、BC于点E、F.若AC=4,BD=8,求四边形ABFE的面积.
应用:如图③,在Rt△ABC中,∠BAC=90°,延长BC到点D,使DC=BC,连结AD.若AC=4,![]() ,则△ABD的面积是 .
,则△ABD的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年是具有里程碑意义的一年,我们将全面建成小康社会,全面建设小康社会的基本标准包括:人均国内生产总值超过3000美元、城镇居民人均可支配收入1.8万元等十个方面.数据“1.8万元”用科学技术法表示为( ).
A.1.8×103元B.1.8×104元C.0.18×105元D.18000元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com