
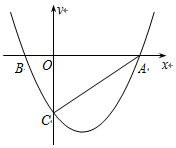
 如图,抛物线y=ax2+bx-2与x轴交于A、B两点,与y轴交于C点,已知A(3,0),且M(1,-$\frac{8}{3}$)是抛物线上另一点.
如图,抛物线y=ax2+bx-2与x轴交于A、B两点,与y轴交于C点,已知A(3,0),且M(1,-$\frac{8}{3}$)是抛物线上另一点.分析 (1)根据题意列方程组即可得到结论;
(2)在y=ax2+bx-2中,当x=0时.y=-2,得到OC=2,如图,设P(0,m),则PC=m+2,OA=3,根据勾股定理得到AC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,①当PA=CA时,则OP1=OC=2,②当PC=CA=$\sqrt{13}$时,③当PC=PA时,点P在AC的垂直平分线上,根据相似三角形的性质得到P3(0,$\frac{5}{4}$),④当PC=CA=$\sqrt{13}$时,于是得到结论;
(3)过H作HG⊥OA于G,设HN交Y轴于M,根据平行线分线段成比例定理得到OM=$\frac{2t}{3}$,求得抛物线的对称轴为直线x=$\frac{-\frac{1}{5}}{2×\frac{5}{3}}$=$\frac{13}{10}$,得到OG=$\frac{13}{10}$,求得GN=t-$\frac{13}{10}$,根据相似三角形的性质得到HG=$\frac{2}{3}$t-$\frac{13}{15}$,于是得到结论.
解答 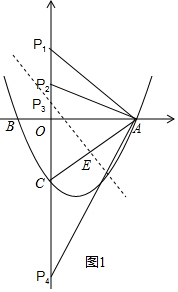 解:(1)把A(3,0),且M(1,-$\frac{8}{3}$)代入y=ax2+bx-2得$\left\{\begin{array}{l}{9a+3b-2=0}\\{a+b-2=-\frac{8}{3}}\end{array}\right.$,
解:(1)把A(3,0),且M(1,-$\frac{8}{3}$)代入y=ax2+bx-2得$\left\{\begin{array}{l}{9a+3b-2=0}\\{a+b-2=-\frac{8}{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=-\frac{4}{3}}\end{array}\right.$;
(2)在y=ax2+bx-2中,当x=0时.y=-2,
∴C(0,-2),
∴OC=2,
如图,设P(0,m),则PC=m+2,OA=3,AC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
①当PA=CA时,则OP1=OC=2,
∴P1(0,2);
②当PC=CA=$\sqrt{13}$时,即m+2=$\sqrt{13}$,∴m=$\sqrt{13}$-2,
∴P2(0,$\sqrt{13}$-2);
③当PC=PA时,点P在AC的垂直平分线上,
则△AOC∽△P3EC,
∴$\frac{\sqrt{13}}{{P}_{3}C}$=$\frac{2}{\frac{\sqrt{13}}{2}}$,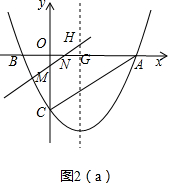
∴P3C=$\frac{13}{4}$,
∴m=$\frac{5}{4}$,
∴P3(0,$\frac{5}{4}$),
④当PC=CA=$\sqrt{13}$时,m=-2-$\sqrt{13}$,
∴P4(0,-2-$\sqrt{13}$),
综上所述,P点的坐标1(0,2)或(0,$\sqrt{13}$-2)或(0,$\frac{5}{4}$)或(0,-2-$\sqrt{13}$);
(3)过H作HG⊥OA于G,设HN交Y轴于M,
∵NH∥AC,
∴$\frac{OM}{OC}=\frac{ON}{OA}$,
∴$\frac{OM}{2}=\frac{t}{3}$,
∴OM=$\frac{2t}{3}$,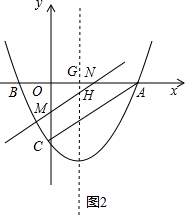
∵抛物线的对称轴为直线x=-$\frac{-\frac{4}{3}}{2×\frac{2}{3}}$=1,
∴OG=1,
①当0<t≤1时,∴GN=1-t,
∵GH∥OC,
∴△NGH∽△NOM,
∴$\frac{HG}{OM}=\frac{GN}{ON}$,
即$\frac{HG}{\frac{2}{3}t}$=$\frac{1-t}{t}$,
∴HG=-$\frac{2}{3}$t+$\frac{2}{3}$,
∴S=$\frac{1}{2}$ON•GH=$\frac{1}{2}$t(-$\frac{2}{3}$t+$\frac{2}{3}$)=-$\frac{1}{3}$t2+$\frac{1}{3}$t(0<t≤1).
②当1<t<3时,
∴GN=t-1,
∵GH∥OC,
∴△NGH∽△NOM,
∴$\frac{HG}{OM}=\frac{GN}{ON}$,
即$\frac{HG}{\frac{2}{3}t}$=$\frac{t-1}{t}$,
∴HG=$\frac{2}{3}$t-$\frac{2}{3}$,
∴S=$\frac{1}{2}$ON•GH=$\frac{1}{2}$t($\frac{2}{3}$t-$\frac{2}{3}$)=$\frac{1}{3}$t2-$\frac{1}{3}$t(1<t<3).
点评 本题考查了待定系数法求得函数的系数,相似三角形的,等腰三角形的判定和性质,三角形的面积公式,掌握的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 事件A和B都是随机事件 | B. | 只有事件B是随机事件 | ||
| C. | 只有事件A是随机事件 | D. | 事件A和B都不是随机事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
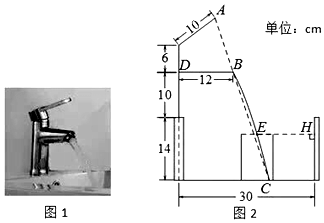
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=3,b=2 | B. | a=-3,b=2 | C. | a=3,b=-1 | D. | a=-1,b=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>$\frac{9}{8}$ | B. | m$>\frac{8}{9}$ | C. | m=$\frac{9}{8}$ | D. | m=$\frac{8}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x+2)2+1 | B. | y=(x+2)2-1 | C. | y=(x-2)2+1 | D. | y=(x-2)2-1 |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年山东省新泰市六年级(五四学制)下学期第一次月考数学试卷(解析版) 题型:填空题
如图所示,图①中的多边形(边数为12)是由等边三角形“扩展”而来的,图②中的多边形是由正方形“扩展”而来的,…,依此类推,则由正n边形“扩展”而来的多边形的边数为( ).
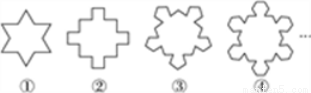
A. n(n-1) B. n(n+1) C. (n+1)(n-1) D. n2+2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com