
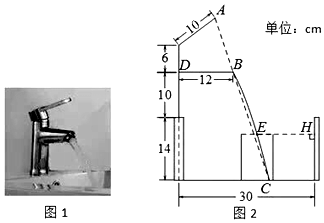
分析 先建立直角坐标系,过A作AG⊥OC于G,交BD于Q,过M作MP⊥AG于P,根据△ABQ∽△ACG,求得C(20,0),再根据水流所在抛物线经过点D(0,24)和B(12,24),可设抛物线为y=ax2+bx+24,把C(20,0),B(12,24)代入抛物线,可得抛物线为y=-$\frac{3}{20}$x2+$\frac{9}{5}$x+24,最后根据点E的纵坐标为10.2,得出点E的横坐标为6+8$\sqrt{2}$,据此可得点E到洗手盆内侧的距离.
解答  解:如图所示,建立直角坐标系,过A作AG⊥OC于G,交BD于Q,过M作MP⊥AG于P,
解:如图所示,建立直角坐标系,过A作AG⊥OC于G,交BD于Q,过M作MP⊥AG于P,
由题可得,AQ=12,PQ=MD=6,故AP=6,AG=36,
∴Rt△APM中,MP=8,故DQ=8=OG,
∴BQ=12-8=4,
由BQ∥CG可得,△ABQ∽△ACG,
∴$\frac{BQ}{CG}$=$\frac{AQ}{AG}$,即$\frac{4}{CG}$=$\frac{12}{36}$,
∴CG=12,OC=12+8=20,
∴C(20,0),
又∵水流所在抛物线经过点D(0,24)和B(12,24),
∴可设抛物线为y=ax2+bx+24,
把C(20,0),B(12,24)代入抛物线,可得
$\left\{\begin{array}{l}{24=144a+12b+24}\\{0=400a+20b+24}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{3}{20}}\\{b=\frac{9}{5}}\end{array}\right.$,
∴抛物线为y=-$\frac{3}{20}$x2+$\frac{9}{5}$x+24,
又∵点E的纵坐标为10.2,
∴令y=10.2,则10.2=-$\frac{3}{20}$x2+$\frac{9}{5}$x+24,
解得x1=6+8$\sqrt{2}$,x2=6-8$\sqrt{2}$(舍去),
∴点E的横坐标为6+8$\sqrt{2}$,
又∵ON=30,
∴EH=30-(6+8$\sqrt{2}$)=24-8$\sqrt{2}$.
故答案为:24-8$\sqrt{2}$.
点评 本题以水龙头接水为载体,考查了二次函数的应用以及相似三角形的应用,在运用数学知识解决问题过程中,关注核心内容,经历测量、运算、建模等数学实践活动为主线的问题探究过程,突出考查数学的应用意识和解决问题的能力,蕴含数学建模,引导学生关注生活,利用数学方法解决实际问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为S=$\sqrt{\frac{1}{4}[{a}^{2}{b}^{2}-(\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2})^{2}]}$.现已知△ABC的三边长分别为1,2,$\sqrt{5}$,则△ABC的面积为1.
我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为S=$\sqrt{\frac{1}{4}[{a}^{2}{b}^{2}-(\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2})^{2}]}$.现已知△ABC的三边长分别为1,2,$\sqrt{5}$,则△ABC的面积为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
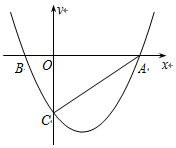 如图,抛物线y=ax2+bx-2与x轴交于A、B两点,与y轴交于C点,已知A(3,0),且M(1,-$\frac{8}{3}$)是抛物线上另一点.
如图,抛物线y=ax2+bx-2与x轴交于A、B两点,与y轴交于C点,已知A(3,0),且M(1,-$\frac{8}{3}$)是抛物线上另一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com