
| 1 |
| 2 |
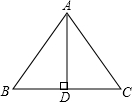 解:如图,∵AD是底边BC上的高,
解:如图,∵AD是底边BC上的高,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 (2012•无锡)如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm).
(2012•无锡)如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm).查看答案和解析>>
科目:初中数学 来源: 题型:
 (2010•资阳)如图,在直角梯形ABCD中,已知AD∥BC,AB=3,AD=1,BC=6,∠A=∠B=90°.设动点P、Q、R在梯形的边上,始终构成以P为直角顶点的等腰直角三角形,且△PQR的一边与梯形ABCD的两底平行.
(2010•资阳)如图,在直角梯形ABCD中,已知AD∥BC,AB=3,AD=1,BC=6,∠A=∠B=90°.设动点P、Q、R在梯形的边上,始终构成以P为直角顶点的等腰直角三角形,且△PQR的一边与梯形ABCD的两底平行.查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江苏无锡卷)数学(带解析) 题型:解答题
如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A.B.C.D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm).
(1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江宁波城区五校联考初三第一学期12月月考数学试卷(解析版) 题型:解答题
如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于上底面上一点)。已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm).

(1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?S最大值是多少?
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江苏无锡卷)数学(解析版) 题型:解答题
如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A.B.C.D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm).
(1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com