
【题目】如图,直线l1的函数表达式为y1=﹣3x+3,且l1与x轴交于点D,直线l2:y2=kx+b经过点A,B,与直线l1交于点C.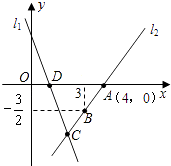
(1)求直线l2的函数表达式及C点坐标;
(2)求△ADC的面积;
(3)当x满足何值时,y1>y2;(直接写出结果)
(4)在直角坐标系中有点E,和A,C,D构成平行四边形,请直接写出E点的坐标.
【答案】
(1)解:∵点A(4,0)、B(3,﹣ ![]() )在直线l2:y2=kx+b上,
)在直线l2:y2=kx+b上,
∴ 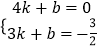 ,
,
解得: 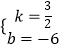 .
.
∴直线l2的解析式为y2= ![]() x﹣6;
x﹣6;
由 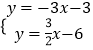 ,
,
解得 ![]() .
.
∴点C的坐标为(2,﹣3)
(2)解:∵点D是直线l1:y=﹣3x+3与x轴的交点,
∴y=0时,0=﹣3x+3,解得x=1,
∴D(1,0),
∵A(4,0),
∴AD=4﹣1=3,
∴△ADC的面积= ![]() ×3×3=
×3×3= ![]()
(3)解:由图象可知,当x<2时,y1>y2
(4)解:符合条件的E点的坐标为E1(5,﹣3)、E2(3,3)、E3(﹣1,﹣3),
①以AC为对角线时,
∵四边形ADCE是平行四边形,
∴CE∥DA,CE=DA=3,
∴将点C(2,﹣3)向右平移3个单位得到点E,即E1(5,﹣3);
②以AD为对角线时,
∵四边形ACDE是平行四边形,
∴CE与AD互相平分,即CE与AD的中点重合,则E2(3,3);
③以CD为对角线时,
∵四边形ADEC是平行四边形,
∴CE∥AD,CE=AD=3,
∴将点C(2,﹣3)向左平移3个单位得到点E,即E3(﹣1,﹣3);
综上所述,符合条件的E点的坐标为E1(5,﹣3)、E2(3,3)、E3(﹣1,﹣3)
【解析】(1)由题意可知直线l2经过点A,B,利用待定系数法建立方程组求解即可;由直线l1的函数表达式和直线l2的函数解析式联立方程,求解即可得出点C的坐标。
(2)先求出点D的坐标,再求出AD的长,然后就可以求出△ADC的面积。
(3)由点C的坐标为(2,﹣3),因此观察直线x=2左右两侧的图像,即可得出y1>y2时,x的取值范围。
(4)此小题分三种情况:①以AC为对角线时;②以AD为对角线时;③以CD为对角线时;根据平行四边形的性质就可以求出满足条件的点E的坐标。
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分)的相关知识才是答题的关键.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】德国《时代》周报网站列举了数据来评价中国改革开放40年的成就,在2017年我国申报了8330项国际专利,目前在年度国际专利申请量排名中位居第五,8330用科学记数法表示为( )
A. 0.833×104B. 83.3×103C. 8.33×103D. 8.33×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x﹣4与抛物线y=ax2+bx+c相交于A,B两点,其中A,B两点的横坐标分别为﹣1和﹣4,且抛物线过原点.
(1)求抛物线的解析式;
(2)在坐标轴上是否存在点C,使△ABC为等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)若点P是线段AB上不与A,B重合的动点,过点P作PE∥OA,与抛物线第三象限的部分交于一点E,过点E作EG⊥x轴于点G,交AB于点F,若S△BGF=3S△EFP,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年“全国助残日”捐款活动中,某班级第一小组7名同学积极捐出自己的零花钱,奉献自己的爱心,他们捐款的数额分别是(单位:元)50、20、50、30、25、50、55,这组数据的众数和中位数分别是( )
A.50元,30元
B.50元,40元
C.50元,50元
D.55元,50元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O.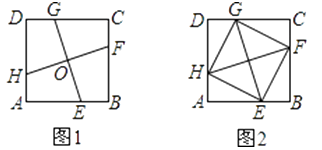
(1)如图2,连接EF,FG,GH,HE,试判断四边形EFGH的形状,并证明你的结论;
(2)将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图3的方式拼接成一个四边形.若正方形ABCD的边长为3cm,HA=EB=FC=GD=1cm,则图3中阴影部分的面积为cm2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班50名学生的处理方式进行统计,得出相关统计表和统计图:

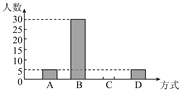
请根据图表所提供的信息回答下列问题:
(1)统计表中的m=_____,n=_____;
(2)补全频数分布直方图;
(3)若该校有2000名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com