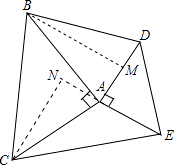
证明:(1)过B作BM⊥DA于M,过C作CN⊥EA交EA的延长线于N,如图,
∵∠BAC=∠DAE=90°,
∴∠BAD+∠CAE=180°,
∵∠CAN+∠CAE=180°,
∴∠BAD=∠CAN
∵sin∠BAD=
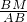
,sin∠CAN=
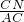
,
又∵AB=AC,
∴BM=CN,
∵DA=AE,
S
△ABD=

DN×BM,S
△ACE=

AE×CN,
∴S
△ADB=S
△ACE.
(2)延长AM到N使AM=QM,连接AQ、EQ,如图,
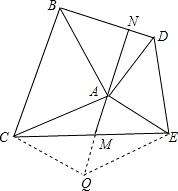
∵AM是△ACE中线,
∴CM=EM,
∴四边形ACQE是平行四边形,
∴AC=EQ=AB,AE=CQ=AD,AC∥EQ,
∴∠CAE+∠AEQ=180°,
∵∠BAD+∠CAE=180°,
∴∠BAD=∠AEQ,
∵在△BAD和△QEA中
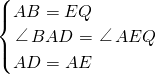
∴△BAD≌△QEA,
∴∠BDA=∠EAM,
∵∠DAE=90°,
∴∠NAD+∠QAE=90°,
∴∠BDA+∠NAD=90°,
∴∠DNA=180°-90°=90°,
∴MN⊥BD.
分析:(1)过B作BM⊥DA于M,过C作CN⊥EA交EA的延长线于N,根据锐角三角函数求出BM=CN,根据三角形的面积公式即可求出答案;
(2)延长AM到N使AM=QN,连接AQ、EQ,求出四边形ACQE是平行四边形,推出AC=EQ=AB,AE=CQ=AD,AC∥EQ,求出∠BAD=∠AEQ,根据SAS证△BAD≌△QEA,推出∠BDA=∠EAN,求出∠BDA+∠NAD=90°,求出∠DNA=90°即可.
点评:本题考查的知识点有全等三角形的性质和判定,三角形的内角和定理,平行四边形的性质和判定,三角形的面积等,主要考查学生运用定理进行推理的能力,题目比较好,综合性比较强.

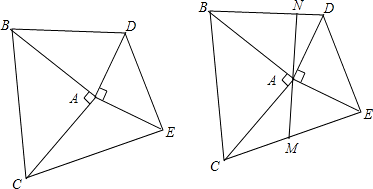 如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE.
如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE. 证明:(1)过B作BM⊥DA于M,过C作CN⊥EA交EA的延长线于N,如图,
证明:(1)过B作BM⊥DA于M,过C作CN⊥EA交EA的延长线于N,如图,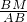 ,sin∠CAN=
,sin∠CAN=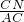 ,
, DN×BM,S△ACE=
DN×BM,S△ACE= AE×CN,
AE×CN,
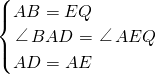


 名校课堂系列答案
名校课堂系列答案 如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“AAS”证明△ABC≌△ABD,则需要加条件
如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“AAS”证明△ABC≌△ABD,则需要加条件