
如图,已知AB⊥BD,CD⊥BD
(1)若AB=9,CD=4,BD=10,请问在BD上是否存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?若存在,求BP的长;若不存在,请说明理由;
(2)若AB=9,CD=4,BD=12,请问在BD上存在多少个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?并求BP的长;
(3)若AB=9,CD=4,BD=15,请问在BD上存在多少个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?并求BP的长;
(4)若AB=m,CD=n,BD=l,请问m,n,l满足什么关系时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的一个P点?两个P点?三个P点?
解:(1)存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
理由是:设BP=x,
∵AB⊥BD,CD⊥BD,∴∠B=∠D=90°。
∴当 或
或 时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
①若 ,则
,则 ,解得:x=
,解得:x= 。
。
②若 ,则
,则 ,即x2﹣10x+36=0,△=(﹣10)2﹣4×1×36<0,此方程无解。
,即x2﹣10x+36=0,△=(﹣10)2﹣4×1×36<0,此方程无解。
∴存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,此时BP的值为 。
。
(2)在BD上存在2个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
理由是:设BP=x,
∵AB⊥BD,CD⊥BD,∴∠B=∠D=90°。
∴当 或
或 时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
①若 ,则
,则 ,解得:x=
,解得:x= 。
。
②若 ,则
,则 ,即x2﹣12x+36=0,解得:x1=x2=6。
,即x2﹣12x+36=0,解得:x1=x2=6。
∴存在2个点P,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,此时BP的值为 或6。
或6。
(3)在BD上存在3个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
理由是:设BP=x,
∵AB⊥BD,CD⊥BD,∴∠B=∠D=90°。
∴当 或
或 时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
①若 ,则
,则 ,解得:x=
,解得:x= 。
。
②若 ,则
,则 ,即x2﹣15x+36=0,解得:x1=3,x2=12。
,即x2﹣15x+36=0,解得:x1=3,x2=12。
∴存在3个点P ,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,此时BP的值为 或3或12。
或3或12。
(4)设BP=x,
∵AB⊥BD,CD⊥BD,∴∠B=∠D=90°。
∴当 或
或 时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
①若 ,则
,则 ,解得:x=
,解得:x=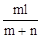 。
。
②若 ,则
,则 ,即x2﹣lx+mn=0。
,即x2﹣lx+mn=0。
∵△=(﹣l)2﹣4×1×mn=l2﹣4mn,
∴当l2﹣4mn<0时,方程没有实数根;当l2﹣4mn=0时,方程有2个相等的实数根;当l2﹣4mn>0时,方程有2个不相等的实数根。
∴当l2﹣4mn<0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的一个P点;
当l2﹣4mn=0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的两个P点;
当l2﹣4mn>0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的三个P点。
解析


科目:初中数学 来源: 题型:解答题
在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.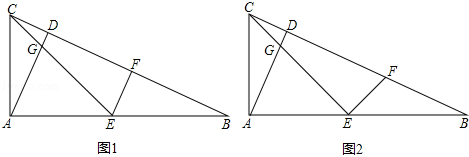
(1)如图1,AC:AB=1:2,EF⊥CB,求证:EF=CD.
(2)如图2,AC:AB=1: ,EF⊥CE,求EF:EG的值.
,EF⊥CE,求EF:EG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图:已知一次函数 的图像分别交
的图像分别交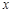 轴、
轴、 轴于
轴于 、
、 两点,且点
两点,且点 在一次函数
在一次函数 的图像上,
的图像上, ⊥
⊥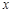 轴于点
轴于点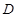 .
.
(1)求 的值及
的值及 、
、 两点的坐标;
两点的坐标;
(2)如果点 在线段
在线段 上,且
上,且 ,求
,求 点的坐标;
点的坐标;
(3)如果点 在
在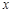 轴上,那么当△
轴上,那么当△ 与△
与△ 相似时,求点
相似时,求点 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,△ABC为等腰直角三角形,∠ACB=90°,F是AC边上的一个动点(点F与A、C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF、AD.
(1)①猜想图1中线段BF、AD的数量关系及所在直线的位置关系,直接写出结论;
②将图1中的正方形CDEF,绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2、图3的情形.图2中BF交AC于点H,交AD于点O,请你判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
(2)将原题中的等腰直角三角形ABC改为直角三角形ABC,∠ACB=90°,正方形CDEF改为矩形CDEF,如图4,且AC=4,BC=3,CD= ,CF=1,BF交AC于点H,交AD于点O,连接BD、AF,求BD2+AF2的值.
,CF=1,BF交AC于点H,交AD于点O,连接BD、AF,求BD2+AF2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在△ABC中,∠C=90°,AC+BC=9,点O是斜边AB上一点,以O为圆心2为半径的圆分别与AC、BC相切于点D、E。
(1)求AC、BC的长;
(2)若AC=3,连接BD,求图中阴影部分的面积(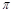 取3.14)。
取3.14)。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在等腰梯形ABCD中,DC∥AB,E是DC延长线上的点,连接AE,交BC于点F。
(1)求证:△ABF∽△ECF
(2)如果AD=5cm,AB=8cm,CF=2cm,求CE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
阅读理解:
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com