
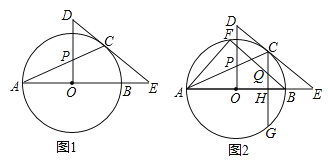
【题目】如图1,AB是⊙O的直径,E是AB延长线上一点,EC切⊙O于点C,OP⊥AO交AC于点P,交EC的延长线于点D.
(1)求证:△PCD是等腰三角形;
(2)CG⊥AB于H点,交⊙O于G点,过B点作BF∥EC,交⊙O于点F,交CG于Q点,连接AF,如图2,若sinE=![]() ,CQ=5,求AF的值.
,CQ=5,求AF的值.
【答案】(1)证明见解析;(2)12.
【解析】
试题分析:(1)连接OC,由切线性质和垂直性质得∠1+∠3=90°、∠2+∠4=90°,继而可得∠3=∠5得证;
(2)连接OC、BC,先根据切线性质和平行线性质及垂直性质证∠BCG=∠QBC得QC=QB=5,而sinE=sin∠ABF=![]() ,可知QH=3、BH=4,设圆的半径为r,在RT在△OCH中根据勾股定理可得r的值,在RT△ABF中根据三角函数可得答案.
,可知QH=3、BH=4,设圆的半径为r,在RT在△OCH中根据勾股定理可得r的值,在RT△ABF中根据三角函数可得答案.
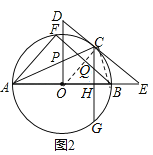
试题解析:(1)连接OC,∵EC切⊙O于点C,∴OC⊥DE,∴∠1+∠3=90°,又∵OP⊥OA,∴∠2+∠4=90°,∵OA=OC,∴∠1=∠2,∴∠3=∠4,又∵∠4=∠5,∴∠3=∠5,∴DP=DC,即△PCD为等腰三角形;
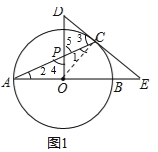
(2)如图2,连接OC、BC.∵DE与⊙O相切于点E,∴∠OCB+∠BCE=90°,∵OC=OB,∴∠OCB=∠OBC,∴∠OBC+∠BCE=90°,又∵CG⊥AB,∴∠OBC+∠BCG=90°,∴∠BCE=∠BCG,∵BF∥DE,∴∠BCE=∠QBC,∴∠BCG=∠QBC,∴QC=QB=5,∵BF∥DE,∴∠ABF=∠E,∵sinE=![]() ,∴sin∠ABF=
,∴sin∠ABF=![]() ,∴QH=3、BH=4,设⊙O的半径为r,∴在△OCH中,
,∴QH=3、BH=4,设⊙O的半径为r,∴在△OCH中,![]() ,解得:r=10,又∵∠AFB=90°,sin∠ABF=
,解得:r=10,又∵∠AFB=90°,sin∠ABF=![]() ,∴AF=12.
,∴AF=12.


科目:初中数学 来源: 题型:
【题目】计算:
(1)(4×104)×(2×103)﹣(6.5×103)×(6×103)
(2)(a﹣1)2+(a+3)(a﹣3)+(a﹣3)(a﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 对角线互相垂直的矩形是正方形
B. 对角线相等的菱形是正方形
C. 有一个角是直角的平行四边形是正方形
D. 一组邻边相等的矩形是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com