(1)解:6;
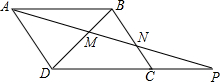
有△AMB∽△PMD,△ADM∽△NBM,△ABN∽△PCN∽△PDA,△ABD≌△CDB,
∴共6对;
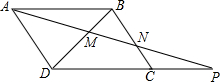
(2)证明:∵AD∥BC,
∴∠ADM=∠NBM,∠DAM=∠BNM,
∴△ADM∽△NBM,
∴
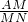
=

;
∵AB∥DC,
∴∠P=∠BAM,∠MDP=∠ABM,
∴△PDM∽△ABM,
∴
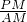
=

,
∴
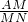
=
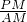
,
∴AM
2=MN•MP;
(3)解:∵AD∥BC,
∴∠PCN=∠PDA,∠P=∠P,
∴△PCN∽△PDA,
∴

=

,
∵DC:CP=2:1,
∴

=

=

;
又∵AD=6
∴NC=2,BN=4.
分析:(1)根据相似三角形的判定定理来做:△ADB∽△CBD、△ABN∽△PCN、△ADM∽△NBM、△AMB∽△PMD、△APD∽△ABN;
(2)由四边形ABCD是平行四边形的性质来证明△ADM∽△NBM、△PDM∽△ABM;再由相似三角形的对应边成比例的性质知:
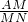
=

、
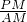
=

,所以AM
2=MN•MP.
(3)由四边形ABCD是平行四边形的性质来证明△PCN∽△PDA;再由相似三角形的对应边成比例的性质知:

=

;最后根据已知条件求解即可.
点评:本题主要考查的是平行四边形的性质:对边平行且相等和内错角相等;相似三角形的判定与性质.

 点M,N.
点M,N.
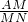 =
= ;
;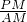 =
= ,
,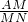 =
=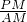 ,
, =
= ,
, =
= =
= ;
;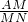 =
= 、
、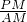 =
= ,所以AM2=MN•MP.
,所以AM2=MN•MP. =
= ;最后根据已知条件求解即可.
;最后根据已知条件求解即可.


 的延长线分别交于点F、E,且
的延长线分别交于点F、E,且
