
【题目】如图,已知抛物线y=ax2+bx+3的图象与x轴交于A、B两点,与y轴交于点C,且点C、D是抛物线上的一对对称点
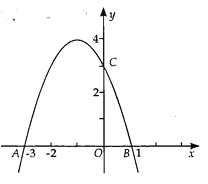
【1】求抛物线的解析式
【2】求点D的坐标,并在图中画出直线BD
【3】求出直线BD的一次函数解析式,并根据图象回答:当x满足什么条件时,上述二次函数的值大于该一次函数的值
【答案】
【1】 ![]()
【2】 D(-2,3) 画出直线BD如图
【3】 BD的解析式为![]() 当-2<x<1时,二次函数的值大于该一次函数的值
当-2<x<1时,二次函数的值大于该一次函数的值

【解析】
(1)将A、B的坐标代入抛物线的解析式中即可求得待定系数的值,
(2)进而可根据抛物线的对称轴求出D点的坐标;
(3)设出直线BD的一次函数解析式为y=kx+b,把B(1,0),D(-2,3)分别代入得可求出k,b,问题的解.由图象可知二次函数的值大于该一次函数的值时:-2<x<1。
解答:
(1)二次函数y=ax2+bx+3的图象经过点A(-3,0),B(1,0)
∴9a-3b+3="0" ,a+b+3=0;解得a=-1 、b=-2;
∴二次函数图象的解析式为y=-x2-2x+3;
(2)∵y=-x2-2x+3,
∴图象与y轴的交点坐标为(0,3)
∵点C、D是抛物线上的一对对称点.对称轴x=-b/2a=-1,
∴D点的坐标为(-2,3).
(3)设直线BD的一次函数解析式为y=kx+b
把B(1,0),D(-2,3)分别代入得:0=k+b、3=-2k+b
解得:k=-1,b=1。
∴BD的解析式为y=-x+1。
由图象可知二次函数的值大于该一次函数的值时:-2<x<1。


科目:初中数学 来源: 题型:
【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同。
(1)从箱子中任意摸出一个球是白球的概率是多少?
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC,AB的垂直平分线交线段AC于D,若△ABC和△DBC的周长分别是60 cm和38 cm,则△ABC的腰长和底边BC的长分别是( )
A. 22cm和16cmB. 16cm和22cm
C. 20cm和16cmD. 24cm和12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ECD均为等边三角形,B、C、D三点在一直线上,AD、BE相交于点F,DF=3,AF=4,则线段FE的长为________.
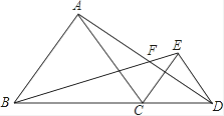
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 单位的速度向点
单位的速度向点![]() 运动,点
运动,点![]() 从点
从点![]() 同时出发,以每秒
同时出发,以每秒![]() 单位的速度向点
单位的速度向点![]() 运动,其中一个动点到达终点时,另一个动点也随之停止运动,设运动时间为
运动,其中一个动点到达终点时,另一个动点也随之停止运动,设运动时间为![]() 秒.
秒.
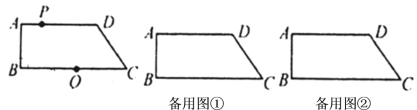
(1)当![]() 时,若以点
时,若以点![]() ,
,![]() 和点
和点![]() ,
,![]() ,
,![]() ,
,![]() 中的两个点为顶点的四边形为平行四边形,且线段
中的两个点为顶点的四边形为平行四边形,且线段![]() 为平行四边形的一边,求
为平行四边形的一边,求![]() 的值.
的值.
(2)若以点![]() ,
,![]() 和点
和点![]() ,
,![]() ,
,![]() ,
,![]() 中的两个点为顶点的四边形为菱形,且线段
中的两个点为顶点的四边形为菱形,且线段![]() 为菱形的一条对角线,请直接写出
为菱形的一条对角线,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车都从A地前往B地,如图分别表示甲、乙两车离A地的距离S(千米)与时间t(分钟)的函数关系.已知甲车出发10分钟后乙车才出发,甲车中途因故停止行驶一段时间后按原速继续驶向B地,最终甲、乙两车同时到达B地,根据图中提供的信息解答下列问题:
(1)甲、乙两车行驶时的速度分别为多少?
(2)乙车出发多少分钟后第一次与甲车相遇?
(3)甲车中途因故障停止行驶的时间为多少分钟?
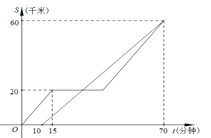
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,以△ABC的一边BC为直径的⊙O分别交AB、AC于D、E,下面判断中:①当△ABC为等边三角形时,△ODE是等边三角形;②当△ODE是等边三角形,△ABC为等边三角形;③当∠A=45°时,△ODE是直角三角形;④当△ODE是直角三角形时,∠A=45°.正确的结论有( )
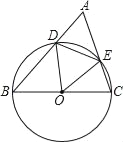
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象开口向上,图象经过点(-1,2)和(1,0),且与y
的图象开口向上,图象经过点(-1,2)和(1,0),且与y
轴相交于负半轴。给出四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论的序
,其中正确结论的序
号是___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.
(1)若∠BAC=60°,∠C=70°,求∠AFB的大小;
(2)若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com