
【题目】如图,二次函数![]() 的图象开口向上,图象经过点(-1,2)和(1,0),且与y
的图象开口向上,图象经过点(-1,2)和(1,0),且与y
轴相交于负半轴。给出四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论的序
,其中正确结论的序
号是___________

【答案】②③④.
【解析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:(1)①由抛物线的开口方向向上可推出a>0,正确;
②因为对称轴在y轴右侧,对称轴为x=-![]() >0,又因为a>0,∴b<0,错误;
>0,又因为a>0,∴b<0,错误;
③由抛物线与y轴的交点在y轴的负半轴上,∴c<0,错误;
④由图象可知:当x=1时y=0,∴a+b+c=0,正确.
故(1)中,正确结论的序号是①④.
(2)①∵a>0,b<0,c<0,∴abc>0,错误;
②由图象可知:对称轴x=-![]() >0且对称轴x=-
>0且对称轴x=-![]() <1,∴2a+b>0,正确;
<1,∴2a+b>0,正确;
③由图象可知:当x=-1时y=2,∴a-b+c=2,当x=1时y=0,∴a+b+c=0;
a-b+c=2与a+b+c=0相加得2a+2c=2,解得a+c=1,正确;
④∵a+c=1,移项得a=1-c,又∵c<0,∴a>1,正确.
故(2)中,正确结论的序号是②③④.
“点睛”二次函数y=ax2+bx+c系数符号的确定:(1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0.(2)b由对称轴和a的符号确定:由对称轴公式x=-![]() 判断符号.(3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0.(4)b2-4ac由抛物线与x轴交点的个数确定:2个交点,b2-4ac>0;1个交点,b2-4ac=0;没有交点,b2-4ac<0.
判断符号.(3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0.(4)b2-4ac由抛物线与x轴交点的个数确定:2个交点,b2-4ac>0;1个交点,b2-4ac=0;没有交点,b2-4ac<0.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)经过A、B、C、D四个点,其中横坐标x与纵坐标y的对应值如下表:
A | B | C | D | |
x | -1 | 0 | 1 | 3 |
y | -1 | 3 | 5 | 3 |
(1)求二次函数解析式;
(2)求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 、
、![]() 分别在射线
分别在射线![]() 、
、![]() 上(点
上(点![]() 不与点
不与点![]() 、点
、点![]() 重合),且保持
重合),且保持![]() .
.
①若点![]() 在线段
在线段![]() 上(如图),且
上(如图),且![]() ,求线段
,求线段![]() 的长;
的长;
②若![]() ,
, ![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产的某种产品按质量分为10个档次,据调研显示,每个档次的日产量及相应的单件利润如下表所示(其中x为正整数,且1≤x≤10):

为了便于调控,此工厂每天只生产一个档次的产品.当生产质量档次为x的产品时,当天的利润为y万元.
(1)求y关于x的函数关系式;
(2)工厂为获得最大利润,应选择生产哪个档次的产品?并求出当天利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
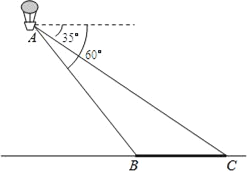
【题目】如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和35°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度.
(结果保留整数,参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() ,
, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com