
【题目】某工厂生产的某种产品按质量分为10个档次,据调研显示,每个档次的日产量及相应的单件利润如下表所示(其中x为正整数,且1≤x≤10):

为了便于调控,此工厂每天只生产一个档次的产品.当生产质量档次为x的产品时,当天的利润为y万元.
(1)求y关于x的函数关系式;
(2)工厂为获得最大利润,应选择生产哪个档次的产品?并求出当天利润的最大值.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
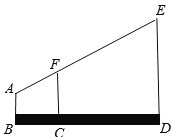
【题目】如图,某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上,已知此人的眼睛到地面的距离AB=1.6m,标杆FC=2.2m,且BC=1m,CD=5m,标杆FC、ED垂直于地面.求电视塔的高ED.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象开口向上,图象经过点(-1,2)和(1,0),且与y
的图象开口向上,图象经过点(-1,2)和(1,0),且与y
轴相交于负半轴。给出四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论的序
,其中正确结论的序
号是___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1, 0)、C(3, 0)、D(3, 4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,以每秒![]() 个单位的速度沿线段AD向点D运动,运动时间为t秒.过点P作PE⊥x轴交抛物线于点M,交AC于点N.
个单位的速度沿线段AD向点D运动,运动时间为t秒.过点P作PE⊥x轴交抛物线于点M,交AC于点N.

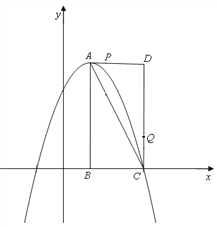
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)当t为何值时,△ACM的面积最大?最大值为多少?
(3)点Q从点C出发,以每秒1个单位的速度沿线段CD向点D运动,当t为何值时,在线段PE上存在点H,使以C、Q、N、H为顶点的四边形为菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形ABCDEF的边长为6cm,P是对角线BE上一动点,过点P作直线l与BE垂直,动点P从B点出发且以1cm/s的速度匀速平移至E点.设直线l扫过正六边形ABCDEF区域的面积为S(cm2),点P的运动时间为t(s),下列能反映S与t之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 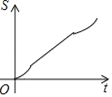
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( ) 
A.a2﹣b2=(a﹣b)2
B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2
D.a2﹣b2=(a+b)(a﹣b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列等式从左到右的变形,属于因式分解的是( )
A.8x2 y3=2x24 y3B.( x+1)( x﹣1)=x2﹣1
C.3x﹣3y﹣1=3( x﹣y)﹣1D.x2﹣8x+16=( x﹣4)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com