
【题目】如图,正六边形ABCDEF的边长为6cm,P是对角线BE上一动点,过点P作直线l与BE垂直,动点P从B点出发且以1cm/s的速度匀速平移至E点.设直线l扫过正六边形ABCDEF区域的面积为S(cm2),点P的运动时间为t(s),下列能反映S与t之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 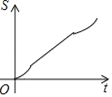
【答案】C
【解析】由题意得:BP=t,
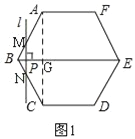
如图1,连接AC,交BE于G,Rt△ABG中,AB=6,∠ABG=60°,∴∠BAG=30°,
∴BG=![]() AB=3,
AB=3,
由勾股定理得:AG=![]() =3
=3![]() ,∴AC=2AG=6
,∴AC=2AG=6![]() ,
,
当0≤t≤3时,PM=![]() t,∴MN=2
t,∴MN=2![]() t,S=S△BMN=
t,S=S△BMN=![]() MNPB=
MNPB=![]() ×
×![]() t2=
t2=![]() t2,
t2,
所以选项A和B不正确;
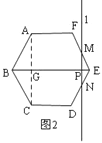
如图2,当9≤t≤12时,PE=12﹣t,
∵∠MEP=60°,∴tan∠MEP=![]() ,∴PM=
,∴PM=![]() (12﹣t),∴MN=2PM=2
(12﹣t),∴MN=2PM=2![]() (12﹣t),
(12﹣t),
∴S=S正六边形﹣S△EMN=2×![]() (AF+BE)×AG﹣
(AF+BE)×AG﹣![]() MNPE=(6+12)×3
MNPE=(6+12)×3![]() ﹣
﹣![]() ×2
×2![]() (12﹣t)(12﹣t)=﹣
(12﹣t)(12﹣t)=﹣![]() t2+24
t2+24![]() t﹣90
t﹣90![]() ,
,
此二次函数的开口向下,
所以选项C正确,选项D不正确;
故选C.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,BC边上有10个不同的点 ![]() ,
, ![]() ,……
,…… ![]() , 记
, 记 ![]() (i = 1,2,……,10),那么
(i = 1,2,……,10),那么 ![]() 的值为( )
的值为( )
A.4
B.14
C.40
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产的某种产品按质量分为10个档次,据调研显示,每个档次的日产量及相应的单件利润如下表所示(其中x为正整数,且1≤x≤10):

为了便于调控,此工厂每天只生产一个档次的产品.当生产质量档次为x的产品时,当天的利润为y万元.
(1)求y关于x的函数关系式;
(2)工厂为获得最大利润,应选择生产哪个档次的产品?并求出当天利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
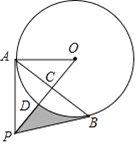
【题目】如图,点A在⊙O上,点P是⊙O外一点,PA切⊙O于点A,连接OP交⊙O于点D,作AB⊥OP于点C,交⊙O于点B,连接PB.
(1)求证:PB是⊙O的切线;
(2)若PC=9,AB=6![]() ,
,
①求图中阴影部分的面积;
②若点E是⊙O上一点,连接AE,BE,当AE=6![]() 时,BE= .
时,BE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
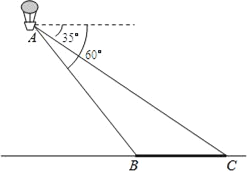
【题目】如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和35°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度.
(结果保留整数,参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() ,
, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学探究课上,老师出示了这样的探究问题,请你一起来探究:
已知:C是线段AB所在平面内任意一点,分别以AC,BC为边,在AB同侧作等边三角形ACE和BCD,联结AD,BE交于点P.
(1)如图1,当点C在线段AB上移动时,线段AD与BE的数量关系是: . 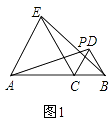
(2)如图2,当点C在直线AB外,且∠ACB<120°,上面的结论是否还成立?若成立请证明,不成立说明理由.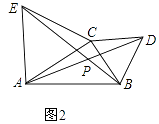
(3)在(2)的条件下,∠APE的大小是否随着∠ACB的大小的变化而发生变化,若变化,写出变化规律,若不变,请求出∠APE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定,“中小学生每天在校体育锻炼时间不小于![]() 小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:
小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:![]() 组:时间小于
组:时间小于![]() 小时;
小时;![]() 组:时间大于等于
组:时间大于等于![]() 小时且小于
小时且小于![]() 小时;
小时;![]() 组:时间大于等于
组:时间大于等于![]() 小时且小于
小时且小于![]() 小时;
小时;![]() 组:时间大于等于
组:时间大于等于![]() 小时.
小时.


根据以上信息,回答下列问题:
(![]() )补全条形统计图和扇形统计图.
)补全条形统计图和扇形统计图.
(![]() )本次调查数据的中位数落在__________组.
)本次调查数据的中位数落在__________组.
(![]() )根据统计数据估计该地区
)根据统计数据估计该地区![]() 名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有多少人?
名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com