
【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( ) 
A.a2﹣b2=(a﹣b)2
B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2
D.a2﹣b2=(a+b)(a﹣b)
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E、F分别是BC,AD上的点,且BE=DF,对角线AC⊥AB. 
(1)求证:四边形AECF是平行四边形;
(2)①当E为BC的中点时,求证:四边形AECF是菱形;
(3)②若AB=6,BC=10,当BE长为时,四边形AECF是矩形. ③四边形AECF有可能成为正方形吗?答: . (填“有”或“没有”)
查看答案和解析>>
科目:初中数学 来源: 题型:
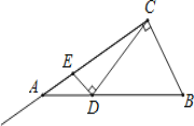
【题目】如图在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=2,D是AB边上的一个动点(不与点A、B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示y与x的函数关系图象大致是( )
A. 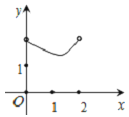 B.
B. 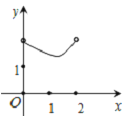 C.
C.  D.
D. 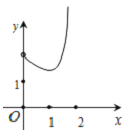
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形. 
(1)请用两种不同的方法求图2中阴影部分的面积(直接用含m,n的代数式表示) 方法1:
方法2:
(2)根据(1)中结论,请你写出下列三个代数式之间的等量关系;代数式:(m+n)2 , (m﹣n)2 , mn
(3)根据(2)题中的等量关系,解决如下问题:已知a+b=8,ab=7,求a﹣b和a2﹣b2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y=x2+bx+c的对称轴为x=2,且其顶点在直线y=﹣2x+2上.
(1)直接写出抛物线的顶点坐标;
(2)求抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com