
【题目】在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 、
、![]() 分别在射线
分别在射线![]() 、
、![]() 上(点
上(点![]() 不与点
不与点![]() 、点
、点![]() 重合),且保持
重合),且保持![]() .
.
①若点![]() 在线段
在线段![]() 上(如图),且
上(如图),且![]() ,求线段
,求线段![]() 的长;
的长;
②若![]() ,
, ![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;

【答案】(1)![]() ;(2)
;(2)![]() ,(0<x<8);
,(0<x<8); ![]() (x≥8)
(x≥8)
【解析】试题分析:(1)求线段CQ的长,根据已知条件AB=AC,∠APQ=∠ABC知道,可以先证明△QCP∽△PBA,由比例关系式得出;
(2)要求y与x之间的函数关系式,以及函数的定义域,需要分两种情况进行讨论:BP在线段CB上,或在CB的延长线上,根据实际情况证明△QCP∽△ABP,根据相似三角形的性质求出比例式,进而得出y与x之间的函数关系式.
解:(1)∵∠APQ+∠CPQ=∠B+∠BAP,∠APQ=∠ABC,
∴∠BAP=∠CQP.
又∵AB=AC,∴∠B=∠C.
∴△CPQ∽△BAP.
∴![]() .
.
∵AB=AC=5,BC=8,BP=6,CP=8﹣6=2,
∴![]() ,
, ![]() .
.
(2)若点P在线段CB上,由(1)知![]() ,
,
∵BP=x,BC=8,∴CP=BC﹣BP=8﹣x,
又∵CQ=y,AB=5,∴![]() ,即
,即![]() .
.
故所求的函数关系式为![]() ,(0<x<8).
,(0<x<8).
若点P在线段CB的延长线上,如图.
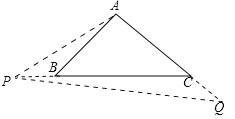
∵∠APQ=∠APB+∠CPQ,
∠ABC=∠APB+∠PAB,∠APQ=∠ABC,
∴∠CPQ=∠PAB.
又∵∠ABP=180°﹣∠ABC,∠PCQ=180°﹣∠ACB,∠ABC=∠ACB,
∴∠ABP=∠PCQ.∴△QCP∽△PBA.∴![]() .
.
∵BP=x,CP=BC+BP=8+x,AB=5,CQ=y,
∴![]() ,即
,即![]() (x≥8).
(x≥8).


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M为⊙O上一点,并且∠BMC=60°.

(1)求证:AB是⊙O的切线;
(2)若E,F分别是边AB,AC上的两个动点,且∠EDF=120°,⊙O的半径为2,试问BE+CF的值是否为定值?若是,求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个命题中是真命题的有( )
①同位角相等②相等的角是对顶角③直角三角形的两个锐角互余④三个内角相等的三角形是等边三角形⑤若|a|=|b|,则a2=b2.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线AM平行于射线BN,∠B=90°,AB=4,C是射线BN上的一个动点,连接AC,作CD⊥AC,且AC=2CD,过C作CE⊥BN交AD于点E,设BC长为a.
(1)求△ACD的面积(用含a的代数式表示);
(2)求点D到射线BN的距离(用含有a的代数式表示);
(3)是否存在点C,使△ACE是以AE为腰的等腰三角形?若存在,请求出此时a的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上,已知此人的眼睛到地面的距离AB=1.6m,标杆FC=2.2m,且BC=1m,CD=5m,标杆FC、ED垂直于地面.求电视塔的高ED.
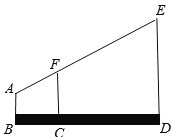
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象开口向上,图象经过点(-1,2)和(1,0),且与y
的图象开口向上,图象经过点(-1,2)和(1,0),且与y
轴相交于负半轴。给出四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论的序
,其中正确结论的序
号是___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列等式从左到右的变形,属于因式分解的是( )
A.8x2 y3=2x24 y3B.( x+1)( x﹣1)=x2﹣1
C.3x﹣3y﹣1=3( x﹣y)﹣1D.x2﹣8x+16=( x﹣4)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com