
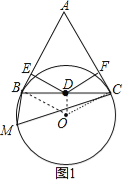
【题目】如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M为⊙O上一点,并且∠BMC=60°.

(1)求证:AB是⊙O的切线;
(2)若E,F分别是边AB,AC上的两个动点,且∠EDF=120°,⊙O的半径为2,试问BE+CF的值是否为定值?若是,求出这个定值;若不是,请说明理由.
【答案】(1)、证明过程见解析;(2)、是定值;定值为![]()
【解析】试题分析:(1)、连结OB、OD、OC,根据D为BC的中点,则OD⊥BC,∠BOD=∠COD,∠ODB=90°,根据∠BMC=![]() ∠BOC得出∠BOD=∠M=60°,则∠OBD=30°,根据△ABC为正三角形得出∠ABC=60°,则∠ABO=90°,即为切线;(2)、作DH⊥AB于H,DN⊥AC于N,连结AD,根据△ABC为正三角形,D为BC的中点则AD平分∠BAC,∠BAC=60°,DH=DN,∠HDN=120°,从而得出△DHE和△DNF全等,则HE=NF,则BE+CF=BH-EH+CN+NF=BH+CN,在Rt△DHB中根据∠DBH=60°得出BH=
∠BOC得出∠BOD=∠M=60°,则∠OBD=30°,根据△ABC为正三角形得出∠ABC=60°,则∠ABO=90°,即为切线;(2)、作DH⊥AB于H,DN⊥AC于N,连结AD,根据△ABC为正三角形,D为BC的中点则AD平分∠BAC,∠BAC=60°,DH=DN,∠HDN=120°,从而得出△DHE和△DNF全等,则HE=NF,则BE+CF=BH-EH+CN+NF=BH+CN,在Rt△DHB中根据∠DBH=60°得出BH=![]() BD,同理得出CN=
BD,同理得出CN=![]() OC,从而得出BE+CF=
OC,从而得出BE+CF=![]() BC,根据BD=OB
BC,根据BD=OB![]() sin30°=
sin30°=![]() 求出BC的长度,从而得出BE+CF为定值
求出BC的长度,从而得出BE+CF为定值![]() .
.
试题解析:(1)、连结OB、OD、OC,如图1, ∵D为BC的中点, ∴OD⊥BC,∠BOD=∠COD,
∴∠ODB=90°, ∵∠BMC=![]() ∠BOC, ∴∠BOD=∠M=60°, ∴∠OBD=30°, ∵△ABC为正三角形,
∠BOC, ∴∠BOD=∠M=60°, ∴∠OBD=30°, ∵△ABC为正三角形,
∴∠ABC=60° ∴∠ABO=60°+30°=90°, ∴AB⊥OB, ∴AB是⊙O的切线;
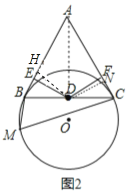
(2)、BE+CF的值是为定值.作DH⊥AB于H,DN⊥AC于N,连结AD,如图2,
∵△ABC为正三角形,D为BC的中点, ∴AD平分∠BAC,∠BAC=60°, ∴DH=DN,∠HDN=120°,
∵∠EDF=120°, ∴∠HDE=∠NDF,在△DHE和△DNF中,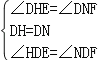 , ∴△DHE≌△DNF,
, ∴△DHE≌△DNF,
∴HE=NF, ∴BE+CF=BH﹣EH+CN+NF=BH+CN, 在Rt△DHB中,∵∠DBH=60°, ∴BH=![]() BD,
BD,
同理可得CN=![]() OC, ∴BE+CF=
OC, ∴BE+CF=![]() OB+
OB+![]() OC=
OC=![]() BC, ∵BD=OB
BC, ∵BD=OB![]() sin30°=
sin30°=![]() , ∴BC=2
, ∴BC=2![]() ,
,
∴BE+CF的值是定值,为![]() .
.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】对于不等式“5x+4y≤20”,我们可以这样解释:香蕉每千克5元,苹果每千克4元,x千克香蕉与y千克苹果的总钱数不超过20元.请你结合生活实际,设计具体情境解释下列不等式:
(1)5x-3y≥2
(2)4a+3b<8.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西西正在参加我市电视台组织的智力竞答节目,只要答对最后两道单选题就能顺利通关,每道单选题都有![]() 、
、![]() 、
、![]() 三个选项.这两道题西西都不会,只能在
三个选项.这两道题西西都不会,只能在![]() 、
、![]() 、
、![]() 三个选项中随机选择一项.
三个选项中随机选择一项.
(![]() )西西答对第一道单选题的概率是__________.
)西西答对第一道单选题的概率是__________.
(![]() )若西西可以使用“求助”(每使用“求助”一次可以让主持人去掉一个错误选项).但是她只有两次“求助”机会,现有两种方案可供西西选择:
)若西西可以使用“求助”(每使用“求助”一次可以让主持人去掉一个错误选项).但是她只有两次“求助”机会,现有两种方案可供西西选择:
方案一:在第一道题中一次性使用两次“求助”机会.
方案二:每道题各使用一次“求助”机会.
请你用画树状图或者列表的方法帮助西西分析哪种方案更有利(三个选项中正确项用“√”表示,错误项用“×”表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后2.5小时追上甲车;
④当甲、乙两车相距50千米时,t=![]() 或
或![]() .
.
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的个数是( )
①单独一个数0不是单项式;②单项式-a的次数为0;③多项式-a2+abc+1是二次三项式;④-a2b的系数是1.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)经过A、B、C、D四个点,其中横坐标x与纵坐标y的对应值如下表:
A | B | C | D | |
x | -1 | 0 | 1 | 3 |
y | -1 | 3 | 5 | 3 |
(1)求二次函数解析式;
(2)求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 、
、![]() 分别在射线
分别在射线![]() 、
、![]() 上(点
上(点![]() 不与点
不与点![]() 、点
、点![]() 重合),且保持
重合),且保持![]() .
.
①若点![]() 在线段
在线段![]() 上(如图),且
上(如图),且![]() ,求线段
,求线段![]() 的长;
的长;
②若![]() ,
, ![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com