
【题目】如图,长方形纸片ABCD中,已知AD=8,AB=6,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,则CE的长为 . 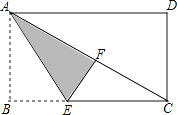
科目:初中数学 来源: 题型:
【题目】为了了解大气污染情况,某学校兴趣小组搜集了2017年上半年中120天郑州市的空气质量指数,绘制了如下不完整的统计图表:
空气质量指数统计表
级别 | 指数 | 天数 | 百分比 |
优 | 0﹣50 | 24 | m |
良 | 51﹣100 | a | 40% |
轻度污染 | 101﹣150 | 18 | 15% |
中度污染 | 151﹣200 | 15 | 12.5% |
重度污染 | 201﹣300 | 9 | 7.5% |
严重污染 | 大于300 | 6 | 5% |
合计 | 120 | 100% |
请根据图表中提供的信息,解答下面的问题:
(1)空气质量指数统计表中的a= ,m= ;
(2)请把空气质量指数条形统计图补充完整:
(3)若绘制“空气质量指数扇形统计图”,级别为“优”所对应扇形的圆心角是 度;
(4)请通过计算估计郑州市2017年中空气质量指数大于100的天数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离为( )
A.4 cmB.5 cmC.小于2 cmD.不大于2 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M为⊙O上一点,并且∠BMC=60°.

(1)求证:AB是⊙O的切线;
(2)若E,F分别是边AB,AC上的两个动点,且∠EDF=120°,⊙O的半径为2,试问BE+CF的值是否为定值?若是,求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在A、B之间有汽车站C站,A、C两地相距540千米,如图1所示.客车由A地驶向C站、货车由B地驶向A地,两车同时出发,匀速行驶,货车的速度是客车速度的![]() .图2是客、货车离C站的路程
.图2是客、货车离C站的路程![]() 、
、![]() (千米)与行驶时间x(小时)之间的函数关系图象.
(千米)与行驶时间x(小时)之间的函数关系图象.
(1)求客、货两车的速度;
(2)求两小时后,货车离C站的路程![]() 与行驶时间x之间的函数关系式;
与行驶时间x之间的函数关系式;
(3)求E点坐标,并说明点E的实际意义.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线AM平行于射线BN,∠B=90°,AB=4,C是射线BN上的一个动点,连接AC,作CD⊥AC,且AC=2CD,过C作CE⊥BN交AD于点E,设BC长为a.
(1)求△ACD的面积(用含a的代数式表示);
(2)求点D到射线BN的距离(用含有a的代数式表示);
(3)是否存在点C,使△ACE是以AE为腰的等腰三角形?若存在,请求出此时a的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com