
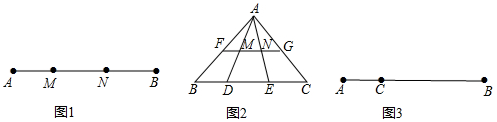
分析 (1)当MN为最大线段时,由勾股定理求出BN;②当BN为最大线段时,由勾股定理求出BN即可;
(2)根据平行线分线段成比例定理得到$\frac{FM}{BD}=\frac{AM}{MD}=\frac{MN}{DE}=\frac{AN}{NE}=\frac{GN}{CE}$=k.根据EC2=BD2+DE2,得到$\frac{1}{{k}^{2}}$GN2=$\frac{1}{{k}^{2}}$FM2+$\frac{1}{{k}^{2}}$MN2,于是得到结论;
(3)①在AB上截取CE=CA;②作AE的垂直平分线,并截取CF=CA;③连接BF,并作BF的垂直平分线,交AB于D;
解答 解:(1)当MN为最大线段时,
∵点M,N是线段AB的勾股分割点,
∴BM=$\sqrt{M{N}^{2}-A{M}^{2}}=\sqrt{16-9}=\sqrt{7}$,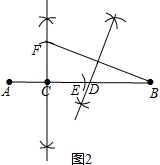
当BN为最大线段时,
∵点M,N是线段AB的勾股分割点,
∴BN=$\sqrt{M{N}^{2}+A{M}^{2}}=\sqrt{16+9}=5$,
综上,BN=$\sqrt{7}$或5;
(2)证明:∵FG∥BC,
∴$\frac{FM}{BD}=\frac{AM}{MD}=\frac{MN}{DE}=\frac{AN}{NE}=\frac{GN}{CE}$=k.
∴FM=kBD,MN=kDE,GN=kCE.
∴EC2=BD2+DE2,
∴$\frac{1}{{k}^{2}}$GN2=$\frac{1}{{k}^{2}}$FM2+$\frac{1}{{k}^{2}}$MN2,
∴NG2=FM2+MN2.
∴点M,N是线段FG的勾股分割点;
(3)作法:①在AB上截取CE=CA;
②作AE的垂直平分线,并截取CF=CA;
③连接BF,并作BF的垂直平分线,交AB于D;
点D即为所求;如图2所示.
点评 本题是三角形综合题目,考查了新定义“勾股分割点”、勾股定理、三角形中位线定理、相似三角形的判定与性质、本题难度较大,综合性强.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
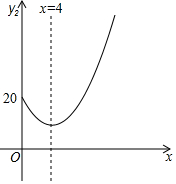 已知某大型超市今年在销售某种水果时,1~6月份的销售单价y1(元/千克)与时间x(月)的关系如表:
已知某大型超市今年在销售某种水果时,1~6月份的销售单价y1(元/千克)与时间x(月)的关系如表:| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y1 | 60 | 30 | 20 | 15 | 12 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com