
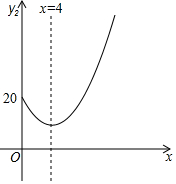
 已知某大型超市今年在销售某种水果时,1~6月份的销售单价y1(元/千克)与时间x(月)的关系如表:
已知某大型超市今年在销售某种水果时,1~6月份的销售单价y1(元/千克)与时间x(月)的关系如表:| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y1 | 60 | 30 | 20 | 15 | 12 | 10 |
分析 (1)根据图表中x、y的乘积是定值60可知此函数是反比例函数,然后写出即可;
(2)根据销售额=单价×销售量求出上半年的销售额,然后根据一次函数的增减性求出上半年最大销售额的月份及最大销售额,根据二次函数的增减性求出下半年的最大销售额与月份,两者比较即可得解;
(3)先求出去年销售额时的最大时的单价,然后根据销售额=单价×销售额表示出销售额总和,列出方程求解即可.
解答 解:(1)∵1×60=60,2×30=60,3×20=60,4×15=60,5×12=60,6×10=60,
∴y1与x成反比例函数关系,
故关系式为y1=$\frac{60}{x}$,
由图可知,抛物线的对称轴为直线x=-$\frac{b}{2}$=4,
解得b=-8,
x=0时,y=c=20,
所以,y2=x2-8x+20;
(2)设销售额为W,则上半年:W1=y1•Z1=$\frac{60}{x}$•(-x2+6x)=-60x+360,
∵1≤x≤6,
∴当x=1时,即1月份的销售额取得最大值,最大值为-60+360=300万元,
下半年:W2=y2•10=10(x2-8x+20)=10(x-4)2+40,
根据二次函数的性质,x>4时,y随x的增大而增大,
∵7≤x≤10,
∴当x=10时,即10月份销售额取得最大值,最大值为=(10-4)2+40=400万元,
∵300<400,
∴去年10月的销售额最大,最大销售额是400万元;
(3)去年7月份销售单价为y2=-72+4×7+41=-49+28+41=20元,
根据题意得,20(1+3a%)×8(1-0.5a%)+(20×3.2)×10(1-0.5a%)=860,去年10月份销售单价为y2=102-8×10+20=40元,
根据题意得,40(1+2a%)×8(1-0.5a%)=360,
整理得,8(a%)2-12a%+1=0,
所以,a%=$\frac{12±\sqrt{112}}{16}$=$\frac{12±10.6}{16}$,
∴a%=1.42或a%=0.09,
∴a=14或a=9,
最大整数值约为14.
点评 此题主要考查了二次函数的应用以及待定系数法求函数的判定与求解,一次函数的增减性,二次函数的增减性,一元二次方程的解法等知识,运用二次函数解决实际问题是中考中热点题型,同学们应重点掌握.


科目:初中数学 来源: 题型:选择题
| A. | 不相交的两条直线叫做平行线 | |
| B. | 点到直线的距离是这点到直线的垂线段 | |
| C. | 过一点有且只有一条直线与已知直线平行 | |
| D. | 在同一平面内,垂直于同一直线的两直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
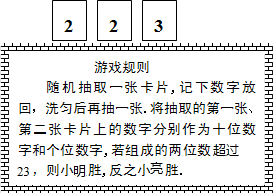 三张背面相同的卡片如图所示,将卡片洗匀后,背面朝上放置在桌面上.小明和小亮用这三张卡片做游戏,游戏规则如图所示,你认为这个游戏公平吗?请列表或画树状图说明理由.
三张背面相同的卡片如图所示,将卡片洗匀后,背面朝上放置在桌面上.小明和小亮用这三张卡片做游戏,游戏规则如图所示,你认为这个游戏公平吗?请列表或画树状图说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
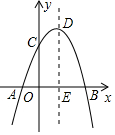 如图,在平面直角坐标系xOy中,抛物线与x轴交于点A(-1,0),B(3,0),与y轴交于点C(0,3),抛物线的顶点为D,对称轴与x轴交于点E.
如图,在平面直角坐标系xOy中,抛物线与x轴交于点A(-1,0),B(3,0),与y轴交于点C(0,3),抛物线的顶点为D,对称轴与x轴交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=0,b≠-1 | B. | a=0,b≠0 | C. | a≠0,b=-1 | D. | a≠0,b≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com