两条直线被一组平行线所截.所得的对应线段成比例．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

17．两条直线被一组平行线所截，所得的对应线段成比例．

分析根据平行线分线段成比例的基本事实可以得到答案．

解答解：根据平行线分线段成比例的基本事实可知，
两条直线被一组平行线所截，所得的对应线段成比例，
故答案为：成比例．

点评本题考查的是平行线分线段成比例的基本事实，掌握两条直线被一组平行线所截，所得的对应线段成比例是解题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

7．在一次有24000名学生参加的数学质量抽测的成绩中，随机取2000名考生的数学成绩进行分析，则在该抽样中，样本指的是（　　）

	A．	所抽取的2000名考生的数学成绩		B．	24000名考生的数学成绩
	C．	2000		D．	2000名考生

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

8．

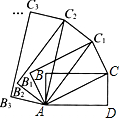如图，在矩形ABCD中，AD=2，CD=1，连接AC，以对角线AC为边，按逆时针方向作矩形ABCD的相似矩形AB₁C₁C，再连接AC₁，以对角线AC₁为边作矩形AB₁C₁C的相似矩形AB₂C₂C₁，…，按此规律继续下去，则矩形AB_nC_nC_n-1的面积为$\frac{{5}^{n}}{{2}^{2n-1}}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

5．

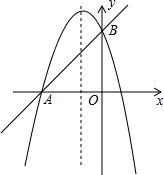如图，已知抛物线y=-x²+bx+c与直线AB相交于A（-3，0），B（0，3）两点．
（1）求这条抛物线的解析式；
（2）设C是抛物线对称轴上的一动点，求使∠CBA=90°的点C的坐标；
（3）探究在抛物线上是否存在点P，使得△APB的面积等于3？若存在，求出点P的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

12．

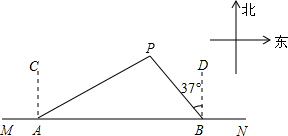如图，船A、B在东西方向的海岸线MN上，均收到已触礁搁浅的船P的求救信号，已知船P在船A的北偏东60°方向上，在船B的北偏西37°方向上，AP=30海里．
（1）尺规作图：过点P作AB所在直线的垂线，垂足为E（要求：保留作图痕迹，不写作法）；
（2）求船P到海岸线MN的距离（即PE的长）；
（3）若船A、船B分别以20海里/时、15海里/时的速度同时出发，匀速直线前往救援，试通过计算判断哪艘船先到达船P处．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

2．比较大小：
（1）-5$\sqrt{3}$与-6$\sqrt{2}$；
（2）$\sqrt{5}$+2与$\sqrt{3}$+$\sqrt{6}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

9．

如图，已知实数a，b在数轴上位置如图所示，试化简$\sqrt{{（a-b）}^{2}}$+$\sqrt{{b}^{2}}$-|a+b|．