
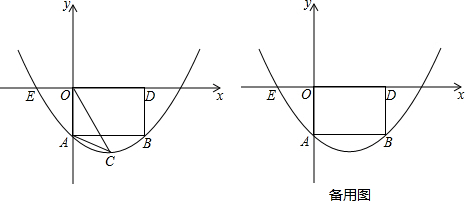
 如图,平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点D,B为AO的中点,DC⊥DB交x轴于点C,E在y轴上,且OC=OE,经过B、E、C三点的抛物线与直线AD交于F、G两点,与其对称轴交于M点
如图,平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点D,B为AO的中点,DC⊥DB交x轴于点C,E在y轴上,且OC=OE,经过B、E、C三点的抛物线与直线AD交于F、G两点,与其对称轴交于M点分析 (1)由条件可以求出点B、E、C的坐标,然后利用待定系数法就可以直接求出抛物线的解析式.
(2)易知△AOD是等腰Rt△,若以P、Q、M为顶点的三角形与△AOD相似,那么△PQM也必须是等腰Rt△;由于∠QPM≠90°,因此本题分两种情况:①PQ为斜边,M为直角顶点;②PM为斜边,Q为直角顶点;
首先求出直线AD的解析式,进而可得到M点的坐标;设出P点横坐标,然后根据抛物线和直线AD的解析式表示出P、Q的纵坐标,即可得到PQ的长;在①中,PQ的长为M、P横坐标差的绝对值的2倍;在②中,PQ的长正好等于M、P横坐标差的绝对值,由此可求出符合条件的P点坐标.
(3)需要分类讨论:当CD为边和当CD为对角线两种情况,利用“平行四边形的对边平行且相等”的性质和点的坐标与图形的性质求得符合条件的点H的坐标.
解答 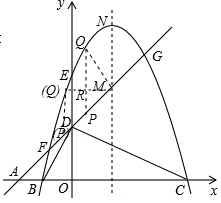 解:(1)在y=x+2中,令x=0,y=0,于是得到A(-2,0),D(0,2),
解:(1)在y=x+2中,令x=0,y=0,于是得到A(-2,0),D(0,2),
∴B(-1,0),
∵BD⊥CD,
∴OD2=OB•OC,
∴C(4,0),E(0,4),设函数解析式为y=a(x+1)(x-4),
∴a×1×(-4)=4,解得a=-1,
∴经过B、E、C三点的抛物线的解析式为:y=-(x+1)(x-4)=-x2+3x+4;
(2)∵A(-2,0),D(0,2);
所以直线AD:y=x+2;
联立$\left\{\begin{array}{l}{y=-{x}^{2}+3x+4}\\{y=x+2}\end{array}\right.$,
解得F(1-$\sqrt{3}$,3-$\sqrt{3}$),G(1+$\sqrt{3}$,3+$\sqrt{3}$);
设P点坐标为(x,x+2)(1-$\sqrt{3}$<x<1+$\sqrt{3}$),则Q(x,-x2+3x+4);
∴PQ=-x2+3x+4-x-2=-x2+2x+2;
由条件容易求得M($\frac{3}{2}$,$\frac{7}{2}$),
若以P、Q、M为顶点的三角形与△AOD相似,则△PQM为等腰直角三角形;
①以M为直角顶点,PQ为斜边;PQ=2|xM-xP|,
即:-x2+2x+2=2($\frac{3}{2}$-x),
解得x=2-$\sqrt{3}$,x=2+$\sqrt{3}$(不合题意舍去)
∴P(2-$\sqrt{3}$,4-$\sqrt{3}$);
②以Q为直角顶点,PM为斜边;PQ=|xM-xQ|,
即:-x2+2x+2=$\frac{3}{2}$-x,
解得x=$\frac{3-\sqrt{11}}{2}$,x=$\frac{3+\sqrt{11}}{2}$(不合题意舍去)
∴P($\frac{3-\sqrt{11}}{2}$,$\frac{7-\sqrt{11}}{2}$)
故存在符合条件的P点,且P点坐标为(2-$\sqrt{3}$,4-$\sqrt{3}$)或($\frac{3-\sqrt{11}}{2}$,$\frac{7-\sqrt{11}}{2}$);
(3)当CD为边时,NH∥CD,NH=CD,
∴xN-xH=±4,
∴xN=$\frac{11}{2}$或xN=-$\frac{5}{2}$.
代入y=-x2+3x+4得yN=-$\frac{31}{4}$,而yN-yH=±2,
∴yH=-$\frac{31}{4}$或yH=-$\frac{47}{4}$,
∴H($\frac{3}{2}$,-$\frac{31}{4}$)或($\frac{3}{2}$,-$\frac{47}{4}$);
若CD为对角线,ND∥CH,ND=CH.
xN-xD=$\frac{5}{2}$
∴xN=$\frac{5}{2}$.
代入y=-x2+3x+4得yN=$\frac{21}{4}$,而yC-yH=yN-yD=$\frac{13}{4}$,
∴yH=-$\frac{13}{4}$,
∴H($\frac{3}{2}$,-$\frac{13}{4}$).
综上所述,共有3个点H满足条件,即($\frac{3}{2}$,-$\frac{31}{4}$)或($\frac{3}{2}$,-$\frac{47}{4}$)或($\frac{3}{2}$,-$\frac{13}{4}$).
点评 本题是二次函数的综合题,考查了待定系数法求二次函数的解析式,相似三角形的判定与性质,同时还考查了分类讨论的数学思想.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30个 | B. | 80个 | C. | 90个 | D. | 120个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
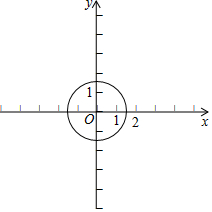 在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),($\sqrt{2}$,$\sqrt{2}$),…,都是梦之点,显然梦之点有无数个.
在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),($\sqrt{2}$,$\sqrt{2}$),…,都是梦之点,显然梦之点有无数个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 10 | D. | 8或10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com