
| A. | 1或-3 | B. | 1或-1 | C. | -1或3 | D. | 3或-3 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016-2017学年湖北省武汉市侏儒山街四校七年级3月月考数学试卷(解析版) 题型:判断题
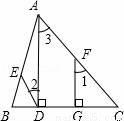
如图,已知AD⊥BC,FG⊥BC,垂足分别为D、G.且∠1=∠2,猜想:∠BDE与∠C有怎样的关系?说明理由.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年福建省泉州市泉港区七年级3月教学质量检测数学试卷(解析版) 题型:单选题
在等式 中,当
中,当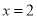 时,
时, 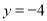 ;当
;当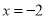 时,
时,  ,则这个等式中
,则这个等式中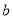 与
与 的值分别是( )
的值分别是( )
A.  =3,
=3, 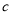 =2 B.
=2 B.  =-3,
=-3, 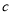 =-2 C.
=-2 C. 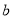 =-3,
=-3,  =2 D.
=2 D.  =3,
=3, 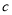 =-2
=-2
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
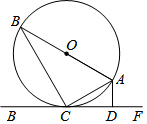 如图,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D.
如图,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com