
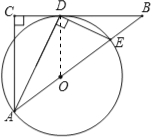
【题目】已知:如图,在![]() 中,
中,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为直径作
为直径作![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OD,由AE为直径、DE⊥AD可得出点D在⊙O上且∠DAO=∠ADO,根据AD平分∠CAB可得出∠CAD=∠DAO=∠ADO,由“内错角相等,两直线平行”可得出AC∥DO,再结合∠C=90°即可得出∠ODB=90°,进而即可证出BC是⊙O的切线;
(2)在Rt△ACB中,利用勾股定理可求出AB的长度,设OD=r,则BO=5﹣r,由OD∥AC可得出![]() ,代入数据即可求出r值,再根据BE=AB﹣AE即可求出BE的长度.
,代入数据即可求出r值,再根据BE=AB﹣AE即可求出BE的长度.
试题解析:(1)证明:连接OD,如图所示.
在Rt△ADE中,点O为AE的中心,
∴DO=AO=EO=![]() AE,∴点D在⊙O上,且∠DAO=∠ADO.
AE,∴点D在⊙O上,且∠DAO=∠ADO.
又∵AD平分∠CAB,∴∠CAD=∠DAO,∴∠ADO=∠CAD,∴AC∥DO.
∵∠C=90°,∴∠ODB=90°,即OD⊥BC.
又∵OD为半径,
∴BC是⊙O的切线;
(2)解:∵在Rt△ACB中,AC=3,BC=4,∴AB=5.
设OD=r,则BO=5﹣r.
∵OD∥AC,∴△BDO∽△BCA,
∴![]() ,即
,即![]() ,解得:r=
,解得:r=![]() ,
,
∴BE=AB﹣AE=5﹣![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,点A的坐标为(﹣2,3),下列说法正确的是( )
A. 点A与点B(2,﹣3)关于x轴对称
B. 点A与点C(﹣3,﹣2)关于x轴对称
C. 点A与点D(2,3)关于y轴对称
D. 点A与点E(3,2)关于y轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村引进甲乙两种水稻良种,各选6块条件相同的实验田,同时播种并核定亩产,结果甲、乙两种水稻的平均产量均为550kg/亩,方差分别为S甲2=141.7,S乙2=433.3,则产量稳定,适合推广的品种为( )
A.甲、乙均可
B.甲
C.乙
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,随着电子商务的快速发展,“电商包裹件”占“快递件”总量的比例逐年增长,根据企业财报,某网站得到如下统计表:
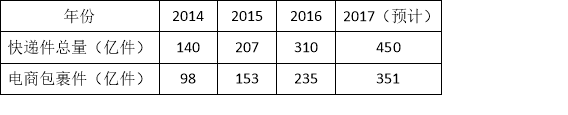
(1)请选择适当的统计图,描述2014﹣2017年“电商包裹件”占当年“快递件”总量的百分比(精确到1%);
(2)若2018年“快递件”总量将达到675亿件,请估计其中“电商包裹件”约为多少亿件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com