
����Ŀ����ͼ��ֱ��y=�� ![]() x+c��x�ύ�ڵ�A��3��0������y�ύ�ڵ�B��������y=��
x+c��x�ύ�ڵ�A��3��0������y�ύ�ڵ�B��������y=�� ![]() x2+bx+c������A��B��
x2+bx+c������A��B��
��1�����B������������ߵĽ���ʽ��
��2��M��m��0��Ϊx����һ���㣬����M�Ҵ�ֱ��x���ֱ����ֱ��AB�������߷ֱ��ڵ�P��N��
�ٵ�M���߶�OA���˶�������B��P��NΪ��������������APM���ƣ����M�����ꣻ
�ڵ�M��x���������˶�����������M��P��N��ǡ��һ�����������������߶ε��е㣨�����غϳ��⣩�����M��P��N����Ϊ����г�㡱����ֱ��д��ʹ��M��P��N�����Ϊ����г�㡱��m��ֵ��
���𰸡�
��1��
�⣺��y=�� ![]() x+c��x�ύ�ڵ�A��3��0������y�ύ�ڵ�B��
x+c��x�ύ�ڵ�A��3��0������y�ύ�ڵ�B��
��0=��2+c�����c=2��
��B��0��2����
��������y=�� ![]() x2+bx+c������A��B��
x2+bx+c������A��B��
�� ![]() �����
����� 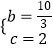 ��
��
�������߽���ʽΪy=�� ![]() x2+
x2+ ![]() x+2
x+2
��2��
�⣺���ɣ�1����ֱ֪�߽���ʽΪy=�� ![]() x+2��
x+2��
��M��m��0��Ϊx����һ���㣬����M�Ҵ�ֱ��x���ֱ����ֱ��AB�������߷ֱ��ڵ�P��N��
��P��m���� ![]() m+2����N��m����
m+2����N��m���� ![]() m2+
m2+ ![]() m+2����
m+2����
��PM=�� ![]() m+2��PA=3��m��PN=��
m+2��PA=3��m��PN=�� ![]() m2+
m2+ ![]() m+2������
m+2������ ![]() m+2��=��
m+2��=�� ![]() m2+4m��
m2+4m��
�ߡ�BPN�͡�APM���ƣ��ҡ�BPN=��APM��
���BNP=��AMP=90����NBP=��AMP=90�㣬
����BNP=90��ʱ������BN��MN��
��BN=OM=m��
�� ![]() =
= ![]() ����
���� ![]() =
=  �����m=0����ȥ����m=2��
�����m=0����ȥ����m=2��
��M��2��0����
����NBP=90��ʱ������ ![]() =
= ![]() ��
��
��A��3��0����B��0��2����P��m���� ![]() m+2����
m+2����
��BP= ![]() =
= ![]() m��AP=
m��AP= ![]() =
= ![]() ��3��m����
��3��m����
�� 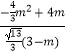 =
= 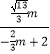 �����m=0����ȥ����m=
�����m=0����ȥ����m= ![]() ��
��
��M�� ![]() ��0����
��0����
���Ͽ�֪����B��P��NΪ��������������APM����ʱ����M������Ϊ��2��0���� ![]() ��0����
��0����
���ɢٿ�֪M��m��0����P��m���� ![]() m+2����N��m����
m+2����N��m���� ![]() m2+
m2+ ![]() m+2����
m+2����
��M��P��N����Ϊ����г�㡱��
����PΪ�߶�MN���е㡢MΪ�߶�PN���е��NΪ�߶�PM���е㣬
��PΪ�߶�MN���е�ʱ������2���� ![]() m+2��=��
m+2��=�� ![]() m2+
m2+ ![]() m+2�����m=3�������غϣ���ȥ����m=
m+2�����m=3�������غϣ���ȥ����m= ![]() ��
��
��MΪ�߶�PN���е�ʱ�����Щ� ![]() m+2+����
m+2+���� ![]() m2+
m2+ ![]() m+2��=0�����m=3����ȥ����m=��1��
m+2��=0�����m=3����ȥ����m=��1��
��NΪ�߶�PM���е�ʱ�����Щ� ![]() m+2=2����
m+2=2���� ![]() m2+
m2+ ![]() m+2�������m=3����ȥ����m=��
m+2�������m=3����ȥ����m=�� ![]() ��
��
���Ͽ�֪��M��P��N�����Ϊ����г�㡱ʱm��ֵΪ ![]() ��1��
��1�� ![]()
����������1����A���������ֱ�߽���ʽ�����c��������B�����꣬��A��B�����꣬���ô���ϵ��������������߽���ʽ����2������M������ɱ�ʾP��N�����꣬�Ӷ��ɱ�ʾ��MA��MP��PN��PB�ij����֡�NBP=90��͡�BNP=90������������ֱ��������������ε����ʿɵõ�����m�ķ��̣������m��ֵ������m�ɱ�ʾ��M��P��N�����꣬�������֪��PΪ�߶�MN���е㡢MΪ�߶�PN���е��NΪ�߶�PM���е㣬�ɷֱ�õ�����m�ķ��̣������m��ֵ��
�����㾫�������ڱ��⿼����߶ε��е�����������ε��ж������ʣ���Ҫ�˽��߶ε��е㵽���˵�ľ�����ȣ����������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ�����ܵó���ȷ�𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���B����C��AD��BC������ΪD��AEƽ����BAC��
��1����֪��B=60������C=30��������DAE�Ķ�����
��2����֪��B=3��C����֤����DAE=��C��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������� ![]() ��x��ĸ����ύ�ڵ�A����y�ύ�ڵ�B������AB����C
��x��ĸ����ύ�ڵ�A����y�ύ�ڵ�B������AB����C ![]() ���������ϣ�ֱ��AC��y�ύ�ڵ�D��
���������ϣ�ֱ��AC��y�ύ�ڵ�D��
��1����c��ֵ��ֱ��AC�ĺ�������ʽ��
��2����P��x����������ϣ���Q��y���������ϣ�����PQ��ֱ��AC���ڵ�M������MO���ӳ���AB�ڵ�N����MΪPQ���е㣮
����֤����APM�ס�AON��
�����M�ĺ�����Ϊm �� ��AN�ij����ú�m�Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���֪������y=ax2+bx��5��x�ύ��A����1��0����B��5��0�����㣬��y�ύ�ڵ�C��
��1���������ߵĺ�������ʽ��
��2������D��y���ϵ�һ�㣬����B��C��DΪ��������������ABC���ƣ����D�����ꣻ
��3����ͼ2��CE��x�����������ཻ�ڵ�E����H��ֱ��CE�·��������ϵĶ��㣬����H����y��ƽ�е�ֱ����BC��CE�ֱ��ڵ�F��G����̽������H�˶����δ�ʱ���ı���CHEF�����������H�����꼰��������
��4������KΪ�����ߵĶ��㣬��M��4��m���Ǹ��������ϵ�һ�㣬��x�ᣬy���Ϸֱ��ҵ�P��Q��ʹ�ı���PQKM���ܳ���С�������P��Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P��![]() ���ڵ�һ���ޣ���a��ȡֵ��Χ�������ϱ�ʾ��ȷ����
���ڵ�һ���ޣ���a��ȡֵ��Χ�������ϱ�ʾ��ȷ����
A��![]() B��
B��![]() C��
C��![]() D��
D��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC �У��� D �DZ� BC �ϵĵ㣨�� B��C ���㲻�غ��������� D�� DE��AC��DF��AB���ֱ� AB��AC �� E��F ���㣬����˵����ȷ���ǣ� ��
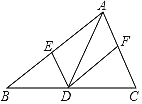
A. �� AD ƽ����BAC�����ı��� AEDF ������
B. �� BD��CD�����ı��� AEDF ������
C. �� AD ��ֱƽ�� BC�����ı��� AEDF �Ǿ���
D. �� AD��BC�����ı��� AEDF �Ǿ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ��
��3��2![]() ��(
��(![]() ��1)2��
��1)2��
��5��2![]() ��(
��(![]() ��
��![]() )2��
)2��
��7��2![]() ��(
��(![]() ��
��![]() )2����
)2����
��1������������Ϲ��ɣ�д����6����ʽ ��
��2����n����ʽ���Ա�ʾΪ ��������֤����õ��ĵ�ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����7��7�����У�ÿ��С�����α߳���Ϊ1�������ʵ���ƽ��ֱ������ϵ��ʹ��A��3��4����C��4��2����

��1���жϡ�ABC����״������ͼ�и���ABC�������
��2����x������һ��P��ʹ��PA+PC��С����PA+PC����СֵΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ʵ�� ![]() ��
�� ![]() ��������ڡ�
��������ڡ� ![]() ����һ���������£�
����һ���������£� ![]() �����磺
�����磺 ![]() ��
�� ![]() ��
��
��1���� ![]() ����
���� ![]() ��ֵ��
��ֵ��
��2���� ![]() ����
���� ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com