
����Ŀ����ƽ��ֱ������ϵ�У�������y=x2+5x+4�Ķ���ΪM����x�ύ��A��B���㣬��y�ύ��C�㡣
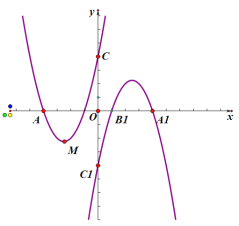
��1�����A��B��C�����ꣻ
��2����������y=x2+5x+4��������ԭ��O�ԳƵ������ߵĺ�������ʽ��
��3���裨2�������������ߵĶ���ΪM1,��x�ύ��A1��B1���㣬��y�ύ��C1�㣬����A��B��C��M��A1��B1��C1��M1��˸����е��ĸ���Ϊ�����ƽ���ı����У�������һ���������ε�ƽ���ı��ε������
���𰸡���1��A��-4��0����B��-1��0����C��0��4������2��y=-x2+5x-4����3��18.
��������
�����������1����y=0�����x��ֵ����x=0�����y�����ɽ��
��2�������A��B��C��������ԭ��O�Գƺ�ĵ�Ϊ��4��0������1��0������0��-4�����ٴ������ʽ�����ɽ��
��3��ȡ�ĵ�A��M��A����M��������AM��MA����A��M����M��A��MM���������ĶԳ��Կ�֪��MM������O��OA=OA����OM=OM�����ɴ��ж��ı���AMA��M��Ϊƽ���ı��Σ���֪AA����MM������ֱ���Ӷ�ƽ���ı���AMA��M���������Σ�����M��MD��x���ڵ�D����������ߵĶ�������M������Sƽ���ı���AMA��M��=2S��AMA�������ɽ��
�����������1����y=0����x2+5x+4=0��
��x1=-4��x2=-1��
��x=0����y=4��
��A��-4��0����B��-1��0����C��0��4����
��2����A��B��C��������ԭ��O�Գƺ�ĵ�Ϊ��4��0������1��0������0��-4����
�����������ߵĺ�������ʽΪy=ax2+bx-4��
����4��0������1��0��������ʽ����![]()
��ã�![]() ��
��
��y=-x2+5x-4��
��3����ͼ��ȡ�ĵ�A��M��A����M��������AM��MA����A��M����M��A��MM����
�����ĶԳ��Կ�֪��MM������O��OA=OA����OM=OM����
���ı���AMA��M��Ϊƽ���ı��Σ�
��֪AA����MM������ֱ��
��ƽ���ı���AMA��M���������Σ�
����M��MD��x���ڵ�D��
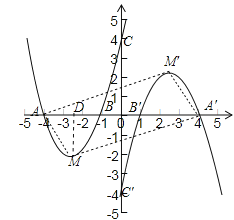
��y=x2+5x+4=(x+![]() )2-
)2-![]() ��
��
��M��-![]() ��-
��-![]() ����
����
����A��-4��0����A����4��0��
��AA��=8��MD=![]() ��
��
��Sƽ���ı���AMA��M��=2S��AMA��=2��![]() ��8��
��8��![]() =18
=18


 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�����������ε����߳��ֱ���2��4����õ��������ε��ܳ�Ϊ��������
A.8��10
B.8
C.10
D.6��12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC�У�AB��AC��8����BAC��30��������ABC�Ƶ�A��ת��ʹ��B����ԭ��ABC�ĵ�C������ʱ��C���ڵ�D�����ӳ��߶�AD����ԭ��ABC�ı�BC���ӳ����ڵ�E����ô�߶�DE�ij�����___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������ε�ÿ���ڽǶ���ȣ��Ҷ�Ϊ160�ȣ����������ε��ڽǺ��ǣ� ����
A. 2520 B. 2880 C. 3060 D. 3240
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ݣ���1��3��2��x��5������Ψһ��������3�����������ݵ���λ����__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֱ�������ε�б�߳���һֱ�DZ߳���2����һֱ�DZ߳�Ϊ6����б�߳�Ϊ��������
A.4
B.8
C.10
D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳����ͼ1����D����ABC���һ�㣬��E��BC�ߵ��ӳ����ϣ�BDƽ����ABC��CDƽ����ACE.��̽����D����A��������ϵ.
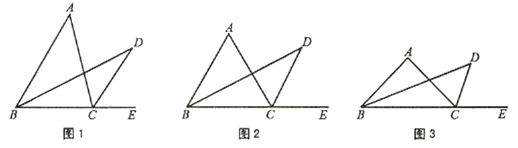
(1)����̽����
��ͼ2������ABC�ǵȱ������Σ������������䣬����D����
��ͼ3������ABC�ǵ��������Σ�������A��100���������������䣬����D����������ͼ�У�����A�����ı��� ��
(2)����֤����
��ͼ1����ABCΪһ�������Σ��ڣ�1���л�õ���D����A�Ĺ�ϵ�Ƿ�����������������ͼ1֤����Ľ��ۣ�����������˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com