
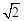 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.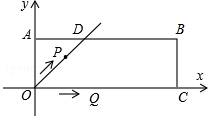
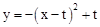 (t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.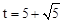 或
或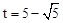 时,△PQB为直角三角形(3)存在t=
时,△PQB为直角三角形(3)存在t=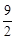 或t=2,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上
或t=2,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上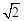 。
。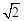 个单位长度,∴t=
个单位长度,∴t=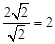 (秒)。
(秒)。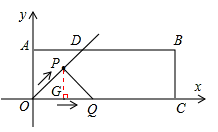
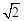 t,∴OG=PG=t。∴点P(t,t)。
t,∴OG=PG=t。∴点P(t,t)。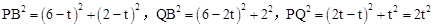 。
。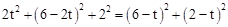 ,
, ,
, 。
。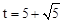 或
或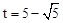 时,△PQB为直角三角形。
时,△PQB为直角三角形。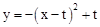 ,得:2t2﹣13t+18=0,解得:t1=
,得:2t2﹣13t+18=0,解得:t1=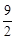 ,t2=2。
,t2=2。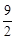 或t=2,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上。
或t=2,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上。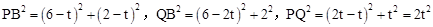 ,再分别就∠PQB=90°和∠PBQ=90°讨论,求出符合题意的t值即可。
,再分别就∠PQB=90°和∠PBQ=90°讨论,求出符合题意的t值即可。

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源:不详 题型:单选题


 或
或
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

A. | B. | C.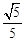 | D. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 点出发,要到距离
点出发,要到距离 点
点
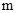 的
的 地去,先沿北偏东
地去,先沿北偏东 方向到达
方向到达 地,然后再沿北偏西
地,然后再沿北偏西 方向走了
方向走了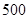
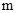 到达目的地
到达目的地 ,此时小霞在营地
,此时小霞在营地 的( )
的( )
A.北偏东 方向上 方向上 | B.北偏东 方向上 方向上 |
C.北偏东 方向上 方向上 | D.?北偏西 方向上 方向上 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.∠A∶∠B∶∠C = 1∶1∶2 | B.a∶b∶c =1∶1∶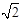 |
C.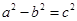 | D.∠A+∠B=2∠C |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com