
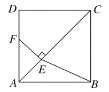
【题目】如图,在正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 上一点,且
上一点,且![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)详见解析;(2)4+4![]()
【解析】
(1)连接CF,利用HL证明Rt△CDF≌Rt△CEF,可得DF=EF,再根据等腰直角三角形可得EF=AF,所以得出DF=AE.
(2) 过点E作EH⊥AB于H,利用勾股定理求出AC,再求出AE,根据特殊直角三角形的边长比求出EH和AH,可得BH,再利用勾股定理求出BE2即可.
(1)连接CF,
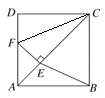
∵∠D=∠CEF=90°,CD=CE,CF=CF,
∴Rt△CDF≌Rt△CEF(HL),
∴DF=EF,
∵AC为正方形ABCD的对角线,
∴∠CAD=45°,
∴△AEF为等腰直角三角形,
∴EF=AF,
∴DF=AE.
(2) ∵AB=2+![]() ,
,
∴由勾股定理得AC=2![]() +2,
+2,
∵CE=CD,
∴AE=![]() .
.
过点E作EH⊥AB于H,则△AEH是等腰直角三角形.
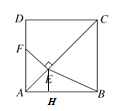
∴EH=AH=![]() AE=
AE=![]() ×
×![]() =1.
=1.
∴BH=2+![]() -1=1+
-1=1+![]() .
.
在Rt△BEH中,BE2=BH2+EH2=(1+![]() )2+12=4+4
)2+12=4+4![]() .
.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边(
表示直角三角形的两直角边(![]() ),下列四个说法:
),下列四个说法:

①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B出发,沿轨道到达C处,在AC上,甲的速度是乙的速度的1.5倍,设t分后甲、乙两遥控车与B处的距离分别为d1,d2(单位:米),则d1,d2与t的函数关系如图,试根据图象解决下列问题.

(1)填空:乙的速度v2=________米/分;
(2)写出d1与t的函数表达式;
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探究什么时间两遥控车的信号不会产生相互干扰?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习完第十二章后,张老师让同学们独立完成课本56页第9题:“如图1,![]() ,
,![]() ,
,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.”
的长.”

(1)请你也独立完成这道题:
(2)待同学们完成这道题后,张老师又出示了一道题:
在课本原题其它条件不变的前提下,将![]() 所在直线旋转到
所在直线旋转到![]() 的外部(如图2),请你猜想
的外部(如图2),请你猜想![]() ,
,![]() ,
,![]() 三者之间的数量关系,直接写出结论:_______.(不需证明)
三者之间的数量关系,直接写出结论:_______.(不需证明)
(3)如图3,将(1)中的条件改为:在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA=
三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA=![]() ,其中
,其中![]() 为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由:
为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由:
查看答案和解析>>
科目:初中数学 来源: 题型:
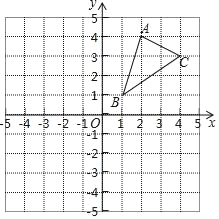
【题目】(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2.
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴交于点C(0,4).
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的一动点,过点M作MN∥y轴交直线BC于点N,当 MN的值最大时,求△BMN的周长.
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=4S2,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电商销售某品牌手表,其成本为每件80元,售价为m元(80<m<240).9月份的销售量为m件,10月份电商对该手表的售价做了调整,在9月份售价的基础上打9折销售,结果销售量增加了50件,销售额增加了5000元.(销售额=销售量×售价)
(1)求该电商9月份销售该品牌手表的销售单价.
(2)11月11日“双十一购物节”,该电商在9月份售价的基础上打折促销(但不亏本),销售的数量y(件)与打折的折数x满足一次函数y=-50x+600.问电商打几折时利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列五个命题:①如果![]() ,那么
,那么![]() ;②内错角相等;③垂线段最短;④带根号的数都是无理数;⑤三角形的一个外角大于任何一个内角.其中真命题的个数为( )
;②内错角相等;③垂线段最短;④带根号的数都是无理数;⑤三角形的一个外角大于任何一个内角.其中真命题的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD的对角线AC将其分割成两个三角形:
(1)如图1.若∠BAC=∠DAC,AB>AD,求证:AB-AD>CB-CD.
(2)如图2.若∠ACD+∠BAC=180°,∠B=∠D,求证:BC=AD.
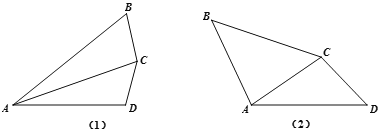
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com