
【题目】某电商销售某品牌手表,其成本为每件80元,售价为m元(80<m<240).9月份的销售量为m件,10月份电商对该手表的售价做了调整,在9月份售价的基础上打9折销售,结果销售量增加了50件,销售额增加了5000元.(销售额=销售量×售价)
(1)求该电商9月份销售该品牌手表的销售单价.
(2)11月11日“双十一购物节”,该电商在9月份售价的基础上打折促销(但不亏本),销售的数量y(件)与打折的折数x满足一次函数y=-50x+600.问电商打几折时利润最大,最大利润是多少?
【答案】(1) 该电商9月份销售该品牌手表的销售单价为200元;(2)当打8折时利润最大,为16000元.
【解析】
(1)根据题意列方程即可得到结论;
(2)根据题意可以列出销售利润的关系式,将其化为顶点式,即可求得最大利润和此时的打折数.
(1)据题意可得:
0.9m( m+50)=m2+5000,
解得:m1=200,m2=250(舍去)..
答:故该电商![]() 月份销售该品牌手表的销售单价为200元;
月份销售该品牌手表的销售单价为200元;
(2)设电商在11月11日购物节销售该品牌的利润为L元,
则:L=200×![]() (-50x+600)-80(-50x+600)(x≥4),
(-50x+600)-80(-50x+600)(x≥4),
L=-1000×x2+16000x-48000=-1000(x-8)2+16000,
当x=8时,最大利润为16000元.
答:商场打8折时利润最大,最大利润是16000元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过点D作DE⊥AC于E.

(1)求证:∠CBP=∠ABP;
(2)若AB-BC=4,AC=8.求AB的长度和DE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
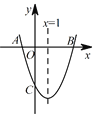
【题目】如图,已知抛物线y=ax2+bx-3的对称轴为直线x=1,交x轴于A,B两点,交y轴于C点,其中B点的坐标为(3,0).
(1)直接写出A点的坐标;
(2)求二次函数y=ax2+bx-3的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,点D是线段AB上的一点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连接DF.给出以下四个结论:①![]() ②若点D是AB的中点,则AF=
②若点D是AB的中点,则AF=![]() AB;③当B,C,F,D四点在同一个圆上时,DF=DB;④若
AB;③当B,C,F,D四点在同一个圆上时,DF=DB;④若![]() ,则
,则![]() ,其中正确的结论序号是( )
,其中正确的结论序号是( )
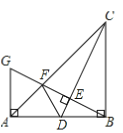
A. ①② B. ③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
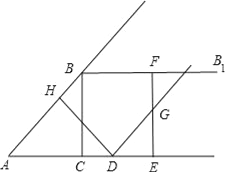
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
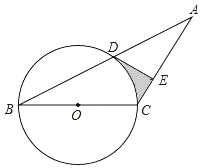
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)若BC=4,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△![]() C;平移△ABC,若A的对应点
C;平移△ABC,若A的对应点![]() 的坐标为(0,4),画出平移后对应的△
的坐标为(0,4),画出平移后对应的△![]() ;
;
(2)若将△![]() C绕某一点旋转可以得到△
C绕某一点旋转可以得到△![]() ,请直接写出旋转中心的坐标;
,请直接写出旋转中心的坐标;
(3)在![]() 轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com