
����Ŀ����ͼ����֪������y=ax2+c���㣨��2��2������4��5����������F��0��2����ֱ��l��y=kx+2�������߽���A��B���㣬��B�ڵ�A���Ҳ࣬����B��x��Ĵ��ߣ�����ΪC��
��1���������ߵĽ���ʽ��
��2������B�����������˶�ʱ���ж��߶�BF��BC��������ϵ����������=������֤������жϣ�
��3��PΪy����һ�㣬��B��C��F��PΪ������ı��������Σ����P��0��m��������Ȼ��m��ֵ��
��4����k=1����ֱ��l�·������������Ƿ���ڵ�Q��ʹ�á�QBF�������������ڣ������Q�����꼰��QBF�����������������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�ѵ㣨��2��2������4��5������y=ax2+c�� ![]() �����
����� ![]() ��
��
���������߽���ʽΪy= ![]() x2+1��
x2+1��
��2��
�⣺BF=BC��
�������£�
��B��x�� ![]() x2+1������F��0��2����
x2+1������F��0��2����
��BF2=x2+�� ![]() x2+1��2��2=x2+��
x2+1��2��2=x2+�� ![]() x2��1��2=��
x2��1��2=�� ![]() x2+1��2��
x2+1��2��
��BF= ![]() x2+1��
x2+1��
��BC��x�ᣬ
��BC= ![]() x2+1��
x2+1��
��BF=BC��
��3��
�⣺��ͼ1��
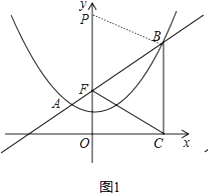
mΪ��Ȼ�������P��F���Ϸ���
����B��C��F��PΪ������ı��������Σ�
��CB=CF=PF��
��CB=FB��
��BC=CF=BF��
���BCFΪ�ȱ������Σ�
���BCF=60�㣬
���OCF=30�㣬
��Rt��OCF��CF=2OF=4��
��PF=CF=4��
��P��0��6����
����Ȼ��m��ֵΪ6��
��4��
�⣺��QE��y�ύAB��E����ͼ2��
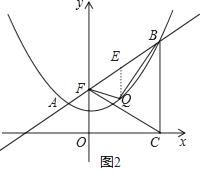
��k=1ʱ��һ�κ�������ʽΪy=x+2��
�ⷽ���� 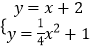 ��
�� ![]() ��
�� ![]() ����B��1+
����B��1+ ![]() ��3+
��3+ ![]() ����
����
��Q��t�� ![]() t2+1������E��t��t+2����
t2+1������E��t��t+2����
��EQ=t+2���� ![]() t2+1��=��
t2+1��=�� ![]() t2+t+1��
t2+t+1��
��S��QBF=S��EQF+S��EQB= ![]() ��1+
��1+ ![]() ��EQ=
��EQ= ![]() ��1+
��1+ ![]() ��������
�������� ![]() t2+t+1��=��
t2+t+1��=�� ![]() ��t��2��2+
��t��2��2+ ![]() +1��
+1��
��t=2ʱ��S��QBF�����ֵ�����ֵΪ ![]() +1����ʱQ������Ϊ��2��2����
+1����ʱQ������Ϊ��2��2����
����������1�����ô���ϵ�����������߽���ʽ����2����B��x�� ![]() x2+1������F��0��2�������������ľ��빫ʽ�õ�BF2=x2+��
x2+1������F��0��2�������������ľ��빫ʽ�õ�BF2=x2+�� ![]() x2+1��2��2=���������䷽���ɵõ�BF=
x2+1��2��2=���������䷽���ɵõ�BF= ![]() x2+1������BC=
x2+1������BC= ![]() x2+1������BF=BC����3����ͼ1���������ε����ʵõ�CB=CF=PF������CB=FB������жϡ�BCFΪ�ȱ������Σ����ԡ�BCF=60�㣬���OCF=30�㣬���ǿɼ����CF=4������PF=CF=4���Ӷ��õ���Ȼ��m��ֵΪ6����4����QE��y�ύAB��E����ͼ2���Ƚⷽ����
x2+1������BF=BC����3����ͼ1���������ε����ʵõ�CB=CF=PF������CB=FB������жϡ�BCFΪ�ȱ������Σ����ԡ�BCF=60�㣬���OCF=30�㣬���ǿɼ����CF=4������PF=CF=4���Ӷ��õ���Ȼ��m��ֵΪ6����4����QE��y�ύAB��E����ͼ2���Ƚⷽ���� 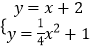 ��B��1+
��B��1+ ![]() ��3+
��3+ ![]() ������Q��t��
������Q��t�� ![]() t2+1������E��t��t+2������EQ=��
t2+1������E��t��t+2������EQ=�� ![]() t2+t+1����S��QBF=S��EQF+S��EQB=
t2+t+1����S��QBF=S��EQF+S��EQB= ![]() ��1+
��1+ ![]() ��EQ=
��EQ= ![]() ��1+
��1+ ![]() ��������
�������� ![]() t2+t+1����Ȼ����ݶ��κ��������ʽ�����⣮
t2+t+1����Ȼ����ݶ��κ��������ʽ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+bx+c��a��0��c��0����x���ڵ�A��B����y���ڵ�C�������A��B��C�����Բ��y�����һ������ΪD��
��1����ͼ1����֪��A��B��C������ֱ�Ϊ����2��0������8��0������0����4����
����������ߵı���ʽ���D�����ꣻ
������MΪ�������ϵ�һ���㣬��λ�ڵ������ޣ����BDM��������ֵ��
��2����ͼ2����a=1����֤������b��cȡ��ֵ����D��Ϊ���㣬����ö������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�Ķ�������ΪA����5��1����B����1��1���� C����1��6����D����5��4�����������ı���ABCD����x�ἰy��ĶԳ�ͼ�Σ���д�����ꡣ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���ACB=90�㣬��D���B��ACͬ�࣬��DAC����BAC����DA=DC������B��BE��DA��DC�ڵ�E��MΪAB���е㣬����MD��ME��
��1����ͼ1������ADC=90��ʱ���߶�MD��ME��������ϵ����
��2����ͼ2������ADC=60��ʱ����̽���߶�MD��ME��������ϵ����֤����Ľ��ۣ�
��3����ͼ3������ADC=��ʱ���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������ǿ��ë������ƹ���������������������˶���ÿλͬѧ������ֻ��ѡ��һ�������˶����Ը�Уѧ�������ȡ10%���е��飬���ݵ��������������²�������Ƶ���ֲ���������ͳ��ͼ��
�˶���Ŀ | Ƶ���������� |
��� | 30 |
���� | a |
ƹ���� | 36 |
���� | b |
���� | 12 |

���������ͼ����Ϣ����������⣺
��1��Ƶ���ֲ����е�a= �� b=��
��2��������ͳ��ͼ�У����������ڵ����ε�Բ�Ľ�Ϊ�ȣ�
��3��ȫУ�ж�����ѧ��ѡ��μ�ƹ�����˶���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=��2����x���һ�������ڣ���3��0���ͣ���4��0��֮�䣬�䲿��ͼ����ͼ��ʾ�������н��ۣ���4a��b=0����c��0���۩�3a+c��0����4a��2b��at2+bt��tΪʵ�������ݵ㣨�� ![]() ��y1��������
��y1�������� ![]() ��y2��������
��y2�������� ![]() ��y3���Ǹ��������ϵĵ㣬��y1��y2��y3 �� ��ȷ�ĸ����У� ��
��y3���Ǹ��������ϵĵ㣬��y1��y2��y3 �� ��ȷ�ĸ����У� �� 
A.4��
B.3��
C.2��
D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AD��BC��D��BD=AD��DG=DC��E��F�ֱ���BG��AC���е㣮 
��1����֤��DE=DF��DE��DF��
��2������EF����AC=10����EF�ij��� 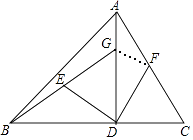
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����УΪ�˽���꼶��ͬѧ����������������������ȡ������ͬѧ������1000���ܲ����ԣ����ճɼ���Ϊ���㡢���á��ϸ��벻�ϸ��ĸ��ȼ���ѧУ���������²�������ͳ��ͼ�� 
��1�����ݸ�������Ϣ����ȫ����ͳ��ͼ��
��2����У���꼶��600������������Ƴɼ�δ�ﵽ�����ж�������
��3��ij��ס�����λ�ɼ������ͬѧ��ѡ�вμӼ������е�ѧУ�˶���1000�ױ�����Ԥ���ֱ�ΪA��B��C������У�ѡ���ɳ�ǩȷ�����飮�ס�������ǡ�÷���ͬһ��ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�������ABC�У�BC=8����D�DZ�AB�㣬��BD=3,��P�DZ�BC��һ���㣬�� ![]() �㣬PE����AC�ڵ�E����CE=ʱ�����������ĵ�P����ֻ��һ����
�㣬PE����AC�ڵ�E����CE=ʱ�����������ĵ�P����ֻ��һ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com